Kinematics: Projectile motion | STPM Physics
Summary
TLDRThis educational video delves into projectile motion, explaining how to solve problems without considering air resistance and the effects of air resistance on motion. It breaks down the motion into horizontal and vertical components, using formulas like 's = vt' for constant velocity and Pythagoras' theorem for velocity magnitude. The video walks through a problem involving a neutron's trajectory, calculating initial velocity, time to reach a detector, and height, concluding that the neutron didn't reach its maximum height in a 100m tunnel. It highlights the impact of air resistance on horizontal deceleration and vertical acceleration, mentioning terminal velocity as an example.
Takeaways
- 📚 The video discusses the second topic in kinematics, which is projectile motion, focusing on solving problems without air resistance and the effects of air resistance on motion.
- 🏐 Projectile motion is the movement of an object in the air under the influence of gravity, which can be seen as an extension of linear motion.
- 🔍 To solve projectile motion problems, the motion is split into vertical and horizontal components, each with its own applicable formulas.
- ⏩ The horizontal component of projectile motion involves constant velocity, and the formula 's = vt' is used to calculate the horizontal displacement or range.
- 📉 The vertical component requires using linear motion equations to find the final vertical velocity, which is influenced by gravity.
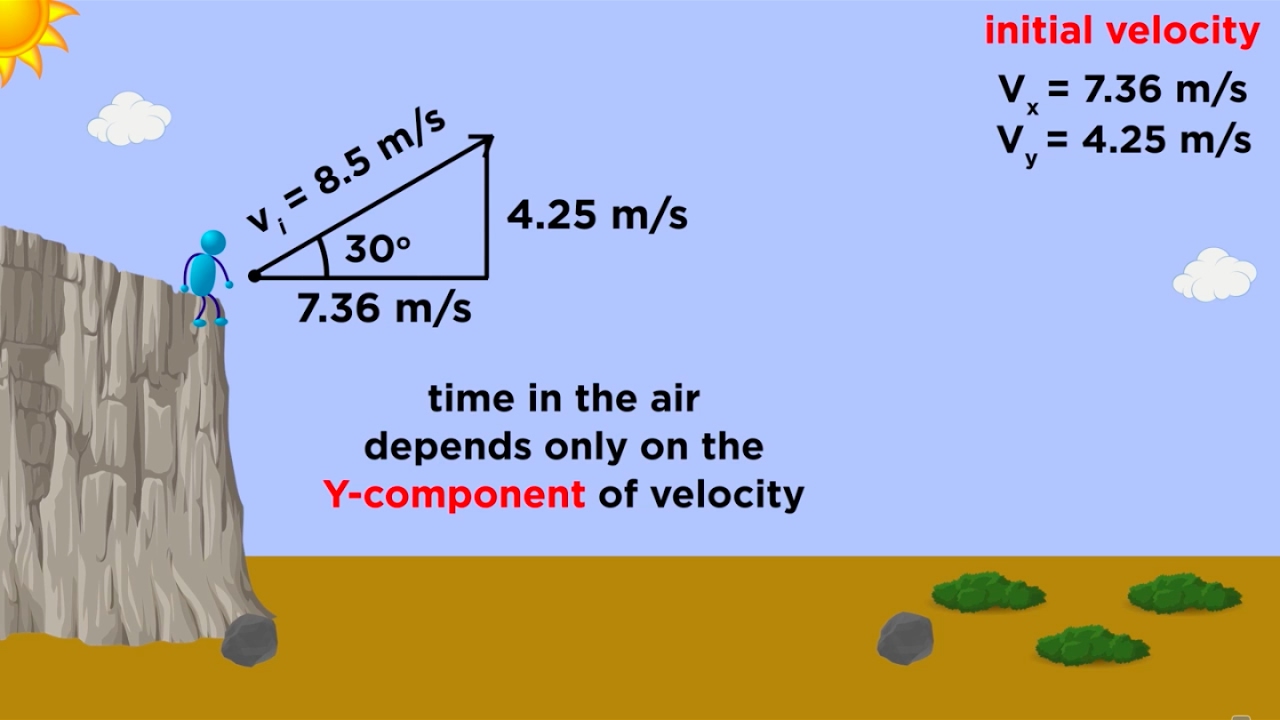
- 📊 Projectile motion problems may ask for the final velocity, which is found by performing vector addition using the Pythagorean theorem and trigonometry.
- 📘 An example from the SMJK Chung Hwa Confucian trial paper in 2022 is used to illustrate solving projectile motion problems with given initial conditions.
- 🔢 The video explains how to resolve initial velocity into horizontal and vertical components and how to use displacement and time to find the initial velocity and time to reach a point.
- 📐 The video also covers how to determine if a neutron has reached its maximum height in a trajectory by comparing times and using formulas to calculate height and range.
- 🌐 The impact of air resistance on projectile motion is discussed, noting that it causes deceleration in horizontal velocity and reduces the acceleration in the vertical direction.
- 🚀 The concept of terminal velocity is mentioned as an example of how air resistance can affect the motion, leading to a constant velocity until the object reaches the ground.
- 📝 The video concludes by emphasizing the importance of understanding projectile motion under gravity's influence and the real-world effects of air resistance.
Q & A
What is the main topic discussed in this video?
-The main topic discussed in this video is projectile motion, specifically how to solve problems on projectile motion without air resistance and the impacts of air resistance on the motion of bodies in air.
How is projectile motion related to linear motion?
-Projectile motion is considered an extension of linear motion. It involves an object moving in a straight line (horizontally) at a constant velocity while simultaneously falling to the ground due to gravity (vertically).
What are the two components of projectile motion?
-The two components of projectile motion are the vertical component, where the object is influenced by gravity and accelerates downwards, and the horizontal component, where the object moves at a constant velocity.
What formula is used to calculate the horizontal displacement in projectile motion?
-The formula used to calculate the horizontal displacement in projectile motion is 's = vt', where 's' is the displacement, 'v' is the horizontal velocity, and 't' is the time.
What is the significance of the final velocity in projectile motion problems?
-The final velocity in projectile motion problems is significant as it represents the object's speed in both the horizontal and vertical components at a given moment. It is found by performing vector addition of the horizontal and vertical velocities.
How can you determine the range of projectile motion?
-The range of projectile motion can be determined by calculating the horizontal displacement using the formula 's = vt', where 's' is the range and 'v' is the constant horizontal velocity.
What is the role of the Pythagoras theorem in solving projectile motion problems?
-The Pythagoras theorem is used to find the magnitude of the final velocity in projectile motion by adding the squares of the horizontal and vertical velocities.
How does air resistance affect the projectile motion?
-Air resistance affects projectile motion by causing deceleration in the horizontal velocity, reducing the expected range, and altering the vertical acceleration, which can result in a longer time to reach the maximum height or the ground.
What is the concept of terminal velocity in the context of projectile motion?
-Terminal velocity is the constant velocity that an object eventually reaches in its descent, where the force of air resistance equals the force of gravity, resulting in zero acceleration.
How can you determine if a projectile has reached its maximum height during its trajectory?
-A projectile has reached its maximum height when its vertical velocity is zero. This can be determined by comparing the time to reach the maximum height with the time to reach other points in the trajectory, such as a detector or the ground.
What is the method to solve for the initial velocity and time to reach a point in projectile motion when given horizontal and vertical displacements?
-To solve for the initial velocity and time, you can use the equations 's = ut' for the horizontal component and 's = ut + 1/2at^2' for the vertical component, where 's' is displacement, 'u' is initial velocity, 'a' is acceleration due to gravity, and 't' is time. By solving these equations simultaneously, you can find the initial velocity and time.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)