Fisica | Sistemas de Referencia & Transformacion de Unidades de Medidas.
Summary
TLDREn este encuentro de física para alumnos de cuarto año, la profesora Josefina Ver Martínez aborda el tema de los sistemas de referencia y transformaciones de unidades. Se define el sistema de referencia como un punto de origen para medir magnitudes físicas como la longitud, y se explica cómo se usan en diferentes dimensiones. Además, se ilustra cómo realizar transformaciones de unidades, utilizando ejemplos como convertir centímetros por segundo cuadrado a metros por minuto cuadrado y kilómetros por hora a metros por segundo, para entender mejor la magnitud física de conceptos como aceleración y velocidad.
Takeaways
- 📚 La clase trata sobre física para alumnos de cuarto año, dirigida por la profesora Josefina Ver Martínez.
- 🎯 El objetivo de la clase es discutir sistemas de referencia y transformaciones de unidades en física.
- 📏 Se define un sistema de referencia como un punto de origen para medir la longitud o magnitud física en un evento.
- 📐 Se menciona que sistemas de referencia pueden ser unidimensionales, bidimensionales o tridimensionales, dependiendo del análisis requerido.
- 📈 Los sistemas de referencia se apoyan en la matemática del plano cartesiano para la representación gráfica de magnitudes físicas.
- 📝 Se destaca la importancia de la elección del sistema de referencia en función de la magnitud física a analizar.
- 🔢 Se discute la transformación de unidades, destacando la necesidad de conocer las equivalencias para realizar conversiónes.
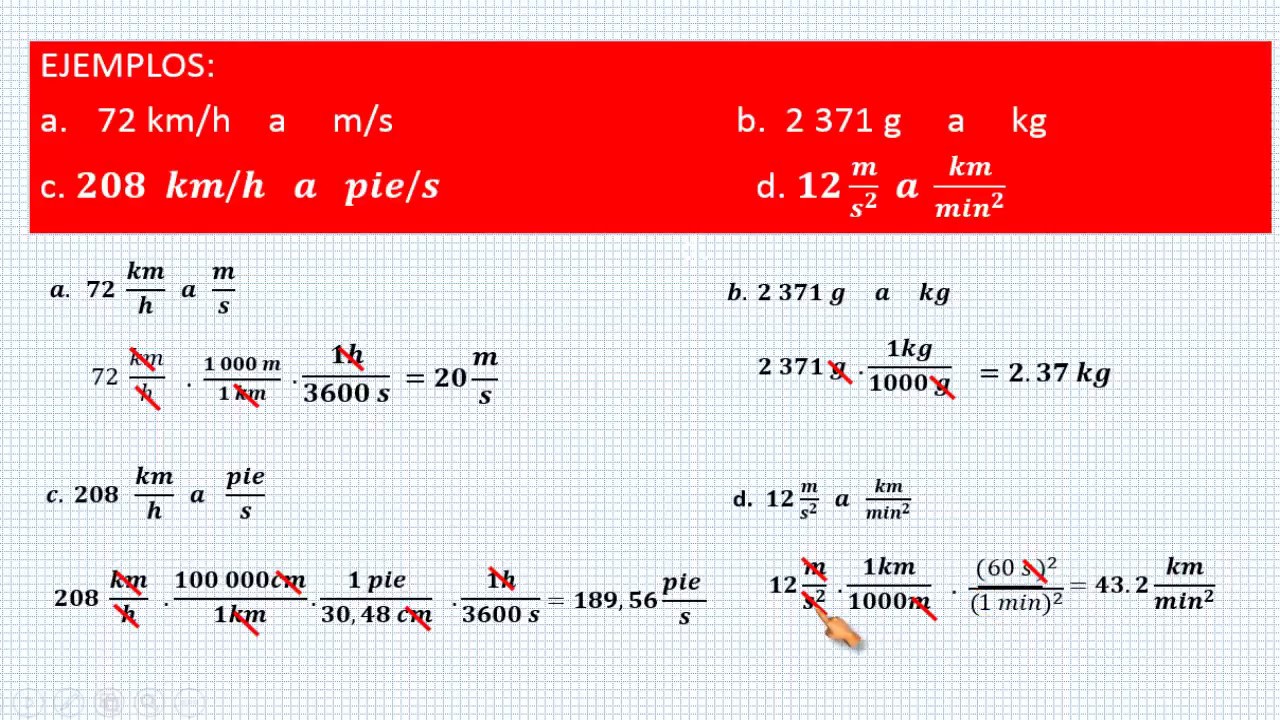
- ⏱ Se da un ejemplo de cómo convertir 'centímetros sobre segundo cuadrado' a 'metros sobre minutos al cuadrado' para la magnitud física de aceleración.
- 🚗 Otro ejemplo muestra la conversión de 'kilómetros por hora' a 'metros por segundo' para la magnitud física de velocidad.
- 📝 Se enfatiza la construcción de factores de conversión para realizar las transformaciones de unidades de manera correcta.
- 🔄 Se describe el proceso de simplificación de unidades y el uso de multiplicaciones y divisiones para llegar a la conversión deseada.
Q & A
¿Qué es el sistema de referencia en física y qué se utiliza para?
-El sistema de referencia es un marco que se utiliza para medir y describir la posición y el movimiento de objetos en el espacio. Se utiliza para analizar la magnitud física de un evento físico, como la longitud, y se elige en función de la magnitud que se desea analizar.
¿Cómo se define la posición en un sistema de referencia?
-La posición se define como un punto que se toma como origen y a través del cual se establece la medida de la longitud o la magnitud física que se quiere analizar.
¿Cuáles son las dimensiones que se pueden utilizar en un sistema de referencia y cómo se representan?
-Los sistemas de referencia pueden ser unidimensionales, bidimensionales o tridimensionales. En una dimensión, se utiliza un solo eje, en dos dimensiones se utiliza un plano cartesiano con ejes x e y, y en tres dimensiones se añade un tercer eje, comúnmente el eje z.
¿Qué es la longitud en física y cómo se mide?
-La longitud es una magnitud física que se refiere a la extensión de un objeto en un eje determinado. Se mide en unidades de longitud como el metro, y en sistemas de referencia se utiliza para graficar y analizar la posición de los objetos.
¿Cómo se calcula el área en un plano cartesiano y cuál es su unidad?
-El área en un plano cartesiano se calcula multiplicando la longitud por la anchura. La unidad de área es el metro cuadrado (m²), que es el producto de metro por metro.
¿Qué es el volumen y cómo se calcula en un sistema tridimensional?
-El volumen es la cantidad de espacio que ocupa un objeto en tres dimensiones. Se calcula multiplicando la longitud, la anchura y la altura. La unidad de volumen es el metro cúbico (m³), que es el producto de metro por metro por metro.
¿Qué son las transformaciones de unidades y para qué se utilizan?
-Las transformaciones de unidades son el proceso de convertir una magnitud medida en una unidad a otra. Se utilizan para facilitar la comparación y el análisis de datos en diferentes sistemas de medida.
¿Cómo se realiza una transformación de unidades de longitud y tiempo en el ejemplo del script?
-Se utiliza la equivalencia de las unidades; por ejemplo, para convertir 60 centímetros por segundo cuadrado a metros por minuto cuadrado, se multiplica 60 por 100 para convertir centímetros a metros y luego por 3600 para convertir segundos al cuadrado a minutos al cuadrado.
¿Qué es la aceleración y cómo se mide?
-La aceleración es la tasa de cambio de velocidad de un objeto. Se mide en unidades de longitud dividido por el tiempo al cuadrado, como metros por segundo cuadrado (m/s²).
¿Cómo se transforma 40 kilómetros por hora a metros por segundo y cuál es el resultado?
-Para transformar kilómetros por hora a metros por segundo, se divide 40 por 3600 (segundos en una hora) y se multiplica por 1000 (metros en un kilómetro), dando como resultado 11,11 metros por segundo.
¿Qué es un factor de conversión y cómo se construye?
-Un factor de conversión es un número que se utiliza para cambiar de una unidad de medida a otra. Se construye utilizando las equivalencias entre las unidades de medida, colocando la unidad que se desea convertir en el numerador y la unidad deseada en el denominador.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)