Poisson's Equation for Beginners: LET THERE BE GRAVITY and How It's Used in Physics | Parth G
Summary
TLDRIn this video, Parth explores Poisson's equation, starting with the mathematical concepts behind it and its physical implications. He explains the significance of the nabla operator and how it applies to partial derivatives, followed by the importance of del squared in vector calculus. Parth also delves into the equation's application in classical gravitation, particularly through Gauss’s Law and the gravitational potential. The video avoids heavy mathematics, focusing instead on providing clear physical intuition for complex concepts, and concludes with a sponsor segment for Skillshare, offering learning resources for a variety of topics.
Takeaways
- 😀 Poisson's equation is a key concept in physics and mathematics, and the video aims to explain it with minimal heavy math.
- 😀 The downward pointing triangle (nabla or del) in the equation represents partial derivatives in the x, y, and z directions, measuring how quantities change across different dimensions.
- 😀 The nabla operator, when squared (del squared), represents the dot product of two del vectors, leading to second-order derivatives in x, y, and z.
- 😀 The poisson equation equates the sum of second derivatives of a function to another function (phi), illustrating a relationship between quantities in space.
- 😀 The video simplifies the understanding of partial derivatives, explaining how they isolate changes in a specific direction while holding other directions constant.
- 😀 Poisson's equation is presented in different forms, including one specific to gravitational studies.
- 😀 The gravitational field of the Earth, derived using Gauss’s law, is used to illustrate Poisson's equation in a practical, physical context.
- 😀 Gauss’s law, expressed in integral form, helps find the gravitational field by adding up the contributions of little area vectors to the gravitational flux.
- 😀 Gauss’s law can be written in differential form, which shows a relationship between the divergence of the gravitational field and the mass density (rho).
- 😀 Poisson's equation is connected to gravitational forces, and using the fact that gravity is a conservative force, the equation is applied to describe the gravitational potential (v).
Q & A
What is Poisson's equation and how is it generally written?
-Poisson's equation is a partial differential equation that describes the relationship between a function and its second derivatives. The general form is written as del squared (Δ) of a function f equals a source term (phi), represented as Δf = phi. The symbols represent mathematical operations, and the equation is used in various physical contexts, including gravitation and electrostatics.
What does the downward pointing triangle (nabla) represent in vector calculus?
-The downward pointing triangle, known as nabla or del, is a vector operator that represents partial derivatives with respect to spatial coordinates. It measures how a quantity changes in the x, y, and z directions. The nabla operator is used to calculate gradients, divergences, and curls of vector fields.
What is the significance of the second derivative (del squared) in Poisson's equation?
-The second derivative (del squared) represents the sum of second-order partial derivatives with respect to spatial coordinates (x, y, z). It quantifies how a function's rate of change is itself changing, providing insights into how the function behaves in different directions. In Poisson's equation, it relates the spatial distribution of a field to a source term.
What does the term 'partial derivative' mean in the context of the Poisson equation?
-A partial derivative measures how a function changes with respect to one of its variables, while keeping the other variables constant. In the context of Poisson's equation, partial derivatives describe how the function (e.g., a potential field) changes in different spatial directions (x, y, z).
How does the concept of 'partial derivatives' relate to the flower distribution example in the video?
-In the video, the flower distribution serves as an example of how a quantity (the amount of flour) changes with respect to spatial coordinates. By taking partial derivatives of the distribution, we measure how the flour density changes along the x, y, or z directions, while holding the other directions constant. This demonstrates the mathematical concept of partial derivatives.
What is the physical meaning of Poisson's equation in the study of gravitation?
-In gravitation, Poisson's equation relates the distribution of mass (or mass density) to the gravitational potential field. The equation states that the second derivatives of the gravitational potential must add up to a term related to the mass distribution, which describes how gravity varies in space.
How does Gauss's law relate to Poisson's equation in gravitation?
-Gauss's law describes the relationship between the gravitational field and the mass enclosed within a surface. By considering the gravitational field as the gradient of a scalar potential, and using the identity for the divergence of a gradient, Gauss's law leads to Poisson's equation. This shows that the gravitational field is determined by the mass distribution, which is the essence of Poisson’s equation in gravitation.
What is the difference between the gravitational potential and gravitational potential energy?
-Gravitational potential is a scalar quantity that represents the potential energy per unit mass at a point in a gravitational field. It differs from gravitational potential energy, which refers to the energy associated with a specific mass at a given location. The potential energy depends on both the mass and the gravitational potential at that point.
What does it mean for a force field to be conservative, and how does this relate to gravitation?
-A conservative force field is one where the work done to move an object between two points is independent of the path taken. In the case of gravitation, this means that the gravitational field can be described as the gradient of a scalar potential. The curl of the gravitational field is zero, indicating that gravity is a conservative force, which allows us to use Poisson's equation to describe the field.
Why is the negative sign important in the gravitational field equation derived from Gauss's law?
-The negative sign in the equation arises because the gravitational field lines point inward, towards the center of the Earth, while the area vectors in Gauss’s law point outward. The dot product between the gravitational field and the area vectors therefore results in a negative value, reflecting the opposite direction of the field and the area vectors.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

CHAMP ET POTENTIEL ÉLECTROSTATIQUES
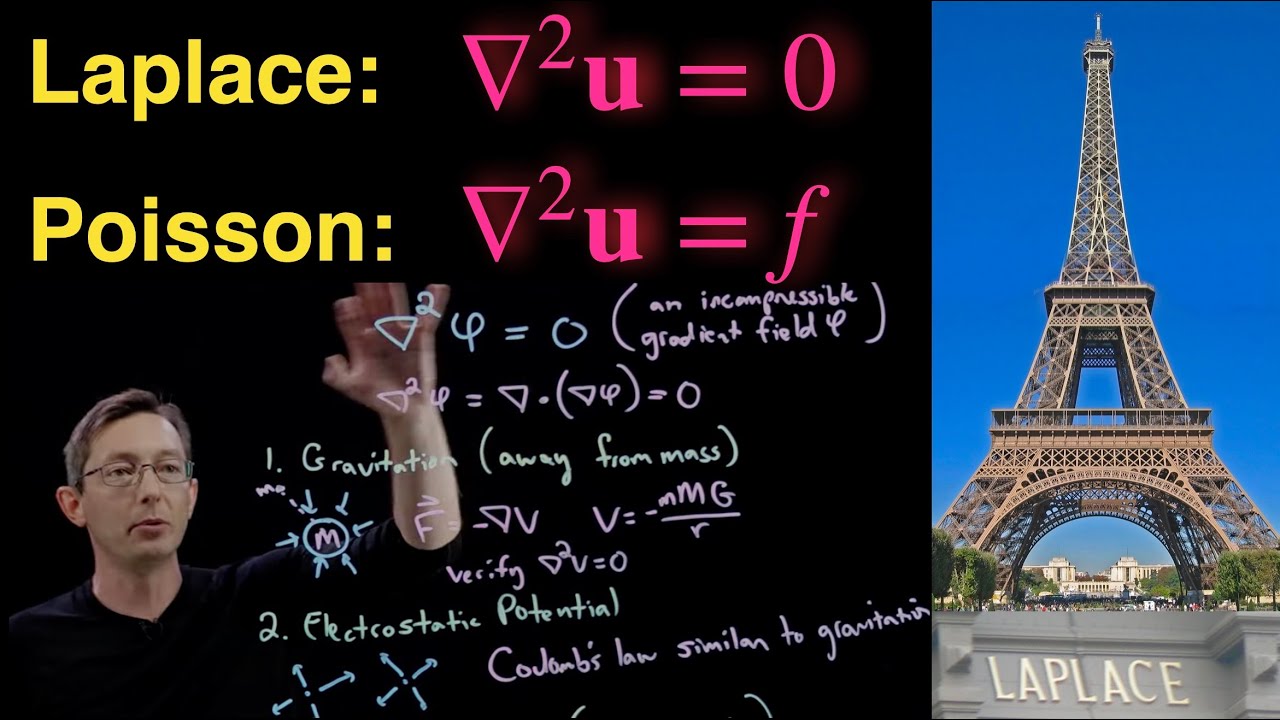
Laplace's Equation and Poisson's Equation

Linearity and nonlinear theories. Schrödinger's equation

Final report-Thermal Conduction
Kinematics: Acceleration Vs Time Graph

The SECOND Most Important Equation in Quantum Mechanics: Eigenvalue Equation Explained for BEGINNERS
5.0 / 5 (0 votes)