💥💥💥Stuff You MUST Know Cold for the AP Calculus AB Exam💥💥💥[EVERYTHING YOU NEED TO KNOW] 2025

Summary

This video provides an in-depth review of essential calculus concepts, focusing on L'Hopital's Rule and integration by parts. The speaker explains how to apply L'Hopital's Rule to resolve indeterminate limits and discusses the steps for using integration by parts to simplify integrals. Key tips for solving problems are provided, including the mnemonic LIPET for selecting the appropriate functions for integration by parts. This review is designed to help students prepare for the AP Calculus exam and final exams, with clear explanations and practical examples.

Takeaways

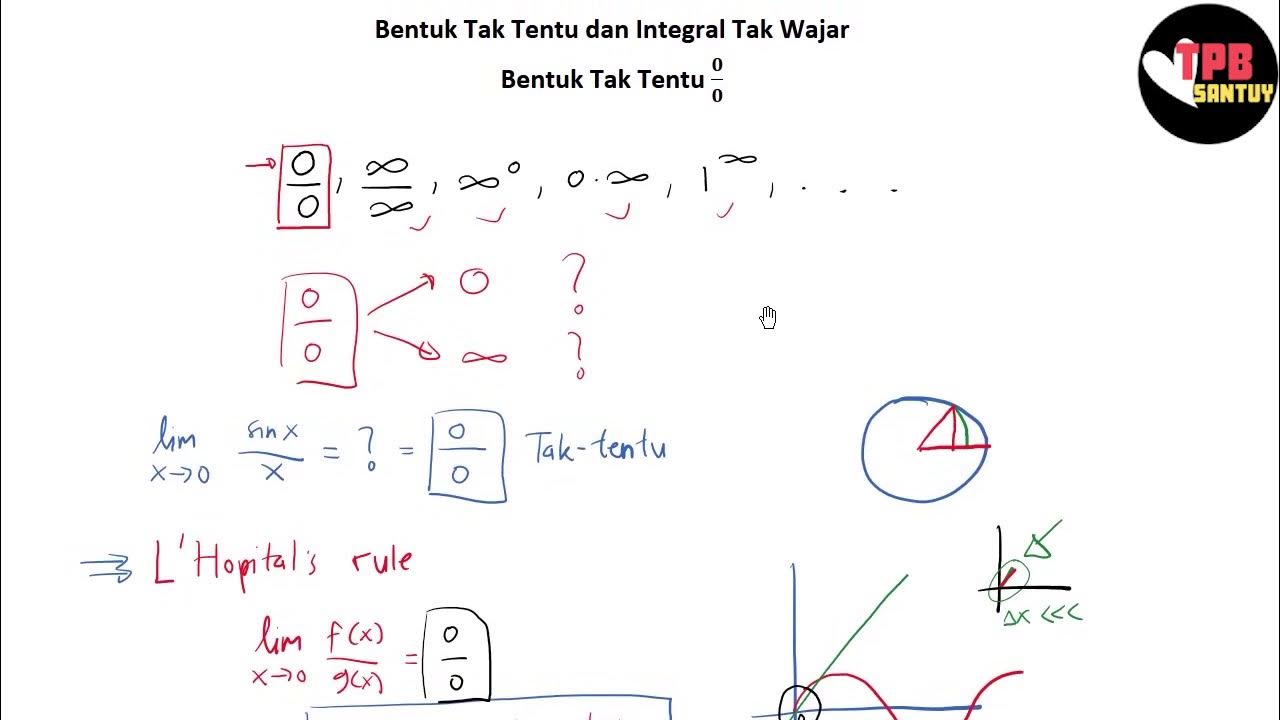
• 😀 L'Hopital's Rule is used to solve limits of indeterminate forms like 0/0 or ∞/∞ by differentiating the numerator and denominator separately.
• 😀 If an indeterminate form involves other operations (like 0 × ∞), algebraic manipulation can help convert it into a fraction for applying L'Hopital's Rule.
• 😀 L'Hopital's Rule can be applied multiple times if the indeterminate form persists after differentiation.
• 😀 Integration by parts is the reverse of the product rule for derivatives and is used to integrate products of functions.
• 😀 The formula for integration by parts is: ∫u dv = uv - ∫v du.
• 😀 Choosing the right 'u' in integration by parts is important for simplification; typically, 'u' is chosen from the order: Logarithmic, Inverse Trigonometric, Algebraic, Trigonometric, Exponential (LIATE).
• 😀 An example of integration by parts: ∫ln(x) dx involves choosing u = ln(x) and dv = dx, leading to the result x ln(x) - x + C.
• 😀 Mastering L'Hopital's Rule and integration by parts is essential for solving problems in limits and integrals in calculus.
• 😀 The review emphasizes these key techniques for success on the AP Calculus exam and final exams.
• 😀 Students should reach out for further clarification if they have questions about specific topics covered in the review.

Q & A

What is L'Hopital's Rule used for in calculus?

L'Hopital's Rule is used to evaluate limits involving indeterminate forms, specifically 0/0 or infinity/infinity. It helps simplify such limits by differentiating the numerator and denominator separately.

How many times can L'Hopital's Rule be applied?

L'Hopital's Rule can be applied multiple times if the result continues to yield an indeterminate form after each application.

What do you do if you encounter indeterminate forms like 0 * infinity or 0^infinity?

If you encounter indeterminate forms like 0 * infinity or 0^infinity, you can algebraically manipulate the expression to convert it into a fraction. Then, L'Hopital's Rule can be applied to the resulting fraction.

What is the purpose of integration by parts?

Integration by parts is a technique used to integrate products of functions, based on the reverse of the product rule for differentiation.

How is the integration by parts formula expressed?

The formula for integration by parts is ∫ u dv = uv - ∫ v du, where u and dv are parts of the integrand that you choose strategically to simplify the integration process.

What is the LIPET rule and how does it help in choosing 'u' and 'dv' for integration by parts?

The LIPET rule is a guideline for choosing 'u' and 'dv' when performing integration by parts. The order of preference is: Logarithmic, Inverse trigonometric, Polynomial, Exponential, and Trigonometric functions. The idea is to choose 'u' from the category that makes differentiation easier and 'dv' from the category that is easier to integrate.

Why is the function ln(x) chosen as 'u' in the integration by parts example?

The function ln(x) is chosen as 'u' because its derivative, 1/x, is simple to compute, which makes it easier to differentiate during the integration by parts process.

What is the result of integrating ln(x) using integration by parts?

The integral of ln(x) is x ln(x) - x + C, where C is the constant of integration.

Can L'Hopital's Rule be applied to all types of limits?

L'Hopital's Rule can only be applied to limits that result in indeterminate forms like 0/0 or infinity/infinity. It is not applicable to other types of limits.

What should you do if you are unsure whether to use L'Hopital's Rule or integration by parts?

If you encounter an indeterminate form in a limit, L'Hopital's Rule is the first choice. If you are dealing with the integration of products of functions, then integration by parts is the correct method. Understanding the specific problem will guide you toward the appropriate technique.