Conjuntos: Introdução (Aula 1 de 4)

Summary

This video provides an introduction to set theory, covering essential concepts such as sets, elements, membership, and the different ways to describe sets. The lecturer explains both finite and infinite sets, with practical examples like the set of vowels, prime numbers, and integers. It also explores unit sets, empty sets, and universal sets, highlighting their importance in mathematics. The video aims to help high school students understand set theory through clear explanations, visual aids, and examples, preparing them for further study and problem-solving in mathematics.

Takeaways

• 😀 Set theory is fundamental in mathematics, as it helps express all mathematical concepts.
• 😀 The lecture consists of four classes on set theory, followed by three problem-solving classes at different levels (basic, intermediate, and advanced).
• 😀 A set is a collection of elements, which can be represented either by listing its elements or by using diagrams like Venn diagrams.
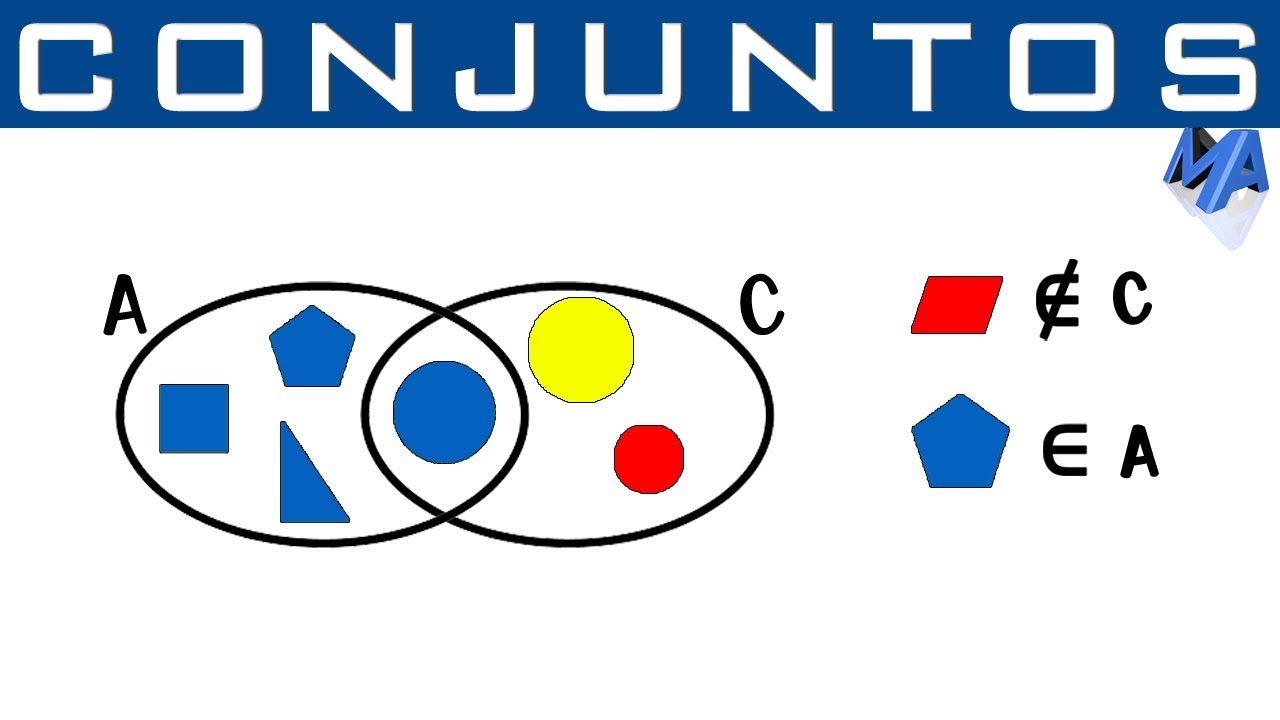
• 😀 The three core concepts in set theory are: 1) Set, 2) Element, and 3) Belonging (Membership), where an element can either belong to a set or not.
• 😀 When an element belongs to a set, it is denoted by the symbol '∈', and when it does not belong, it is denoted by '∉'.
• 😀 A set can be finite (with a specific number of elements) or infinite (with an uncountable number of elements).
• 😀 Describing a set can be done either by listing its elements or by defining it with a property, such as 'x is a divisor of 5'.
• 😀 The empty set is a set with no elements, represented by '∅' or '{}'. It is not the same as a unit set, which contains exactly one element.
• 😀 The universal set contains all elements relevant to a given context (e.g., all real numbers when solving real-number equations).
• 😀 Set notation allows for concise representation of sets, and infinite sets often use ellipses ('...') to indicate continuation, as seen in prime numbers and number ranges.

Q & A

What are the three basic notions in set theory that are accepted without definition?

The three basic notions in set theory are: the notion of a set, the notion of an element, and the notion of membership (pertinence) between an element and a set.

How are sets typically expressed in set theory?

Sets can be expressed either by listing their elements between curly braces (e.g., {1, 2, 3, 4}) or by using a diagram, where elements are represented by points within a closed line.

What does it mean for an element to belong to a set?

If an element is inside a set, it is said to belong to that set. This is called membership, and it is indicated by the symbol '∈'. Conversely, if an element is not part of a set, it is indicated by '∉'.

What is the difference between a finite set and an infinite set in terms of notation?

A finite set lists all its elements explicitly, while an infinite set uses ellipses '…' to indicate that the set continues indefinitely, showing that it has an infinite number of elements.

What is the role of the 'universal set' in set theory?

The universal set, denoted by U, includes all the elements that are being considered within a particular mathematical discussion. It depends on the context, such as the set of all real numbers or all integers, depending on the problem at hand.

How do we describe a set using a property?

A set can be described using a property that its elements satisfy. For example, a set of numbers can be defined as 'the set of numbers x such that x is a divisor of 5.' This defines the set based on a specific property.

What is a unitary set in set theory?

A unitary set is a set that contains exactly one element. For example, the set {4} is a unitary set because it contains only the number 4.

What is a 'null set' or 'empty set'?

A null set, or empty set, is a set that contains no elements. It is denoted as '{}' or '∅'. It can also be described by a property that no element satisfies, such as 'the set of odd numbers divisible by 2.'

What does it mean when a set is described as 'infinite'?

An infinite set is a set that has no end, meaning it continues indefinitely. For example, the set of prime numbers is infinite because there are infinitely many prime numbers.

What is the significance of 'elements' in set theory?

In set theory, elements are the individual objects that belong to a set. These can be numbers, letters, or even other sets. Elements are crucial because the entire concept of a set is based on grouping these individual elements together.