Área de pirâmide - Brasil Escola

Summary

In this educational video, the math instructor explains how to calculate the surface area of a pyramid, specifically focusing on pyramids with a square base. The video introduces key elements such as base edges, lateral edges, height, apothem, and radius, emphasizing the importance of understanding these components. Through a step-by-step example, the instructor demonstrates how to calculate the area of the base and the lateral surface, ultimately leading to the total surface area. The instructor also shares useful tips and shortcuts, including the application of the Pythagorean theorem for quicker calculations, ensuring viewers grasp the essential concepts with ease.

Takeaways

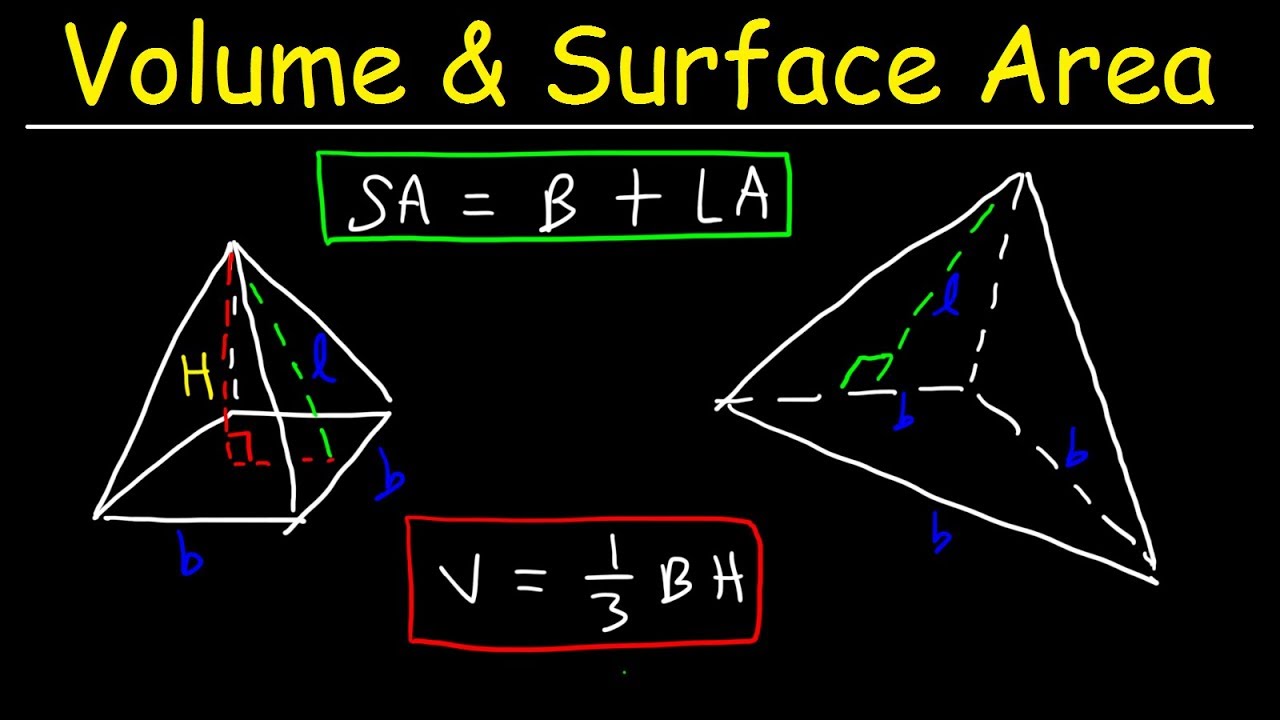
• 😀 The area of a pyramid depends on its type, and there is no single formula for calculating it.
• 😀 For a square-based pyramid, you need to know elements like the base edge length (L), lateral edge (L'), height (h), base apothem (a_b), pyramid apothem (a_p), and base radius (R_b).
• 😀 The total area of a pyramid is the sum of the area of the base and the lateral area, where lateral area is the sum of the areas of the triangles forming the sides.
• 😀 In the case of a square-based pyramid, the total area is found by calculating the area of the square base and the areas of four triangles, then summing them up.
• 😀 For a hexagonal-based pyramid, the process is similar, but involves a hexagon and six triangles.
• 😀 The base apothem is the distance from the center of the base polygon to the midpoint of one side, while the pyramid apothem is the height of the lateral face triangles.
• 😀 The lateral area of a pyramid is calculated by multiplying the area of one triangle by the number of triangles that form the sides of the pyramid.
• 😀 When solving problems involving pyramids, you often need to use the Pythagorean theorem to find missing dimensions such as the height of the triangles.
• 😀 The Pythagorean theorem is essential for solving right triangles formed by the height of the pyramid, the apothem of the base, and the slant height of the pyramid.
• 😀 To calculate the area of the pyramid in the provided example, the area of the base (576 cm²) and the lateral area (960 cm²) were found, resulting in a total area of 1536 cm².

Q & A

What is the main topic of this lesson?

The main topic of the lesson is calculating the area of a pyramid, specifically pyramids with square and hexagonal bases.

Why is there no single formula for calculating the area of a pyramid?

There is no single formula for calculating the area of a pyramid because the calculation depends on the shape of the pyramid's base, which varies from one pyramid to another.

What are the key elements needed to calculate the area of a pyramid?

The key elements needed to calculate the area of a pyramid include the side length of the base (L), the lateral edge (L', which is the slant height), the height of the pyramid (h), the apothem of the base (a_b), the apothem of the pyramid (a_p), and the radius of the base (r_b).

What does the total area of a pyramid consist of?

The total area of a pyramid is the sum of the area of the base and the lateral area, which is the area of the triangles forming the sides of the pyramid.

How is the lateral area of a pyramid calculated?

The lateral area of a pyramid is calculated by finding the area of one triangular face and multiplying it by the number of triangular faces (usually 4 for a square-based pyramid). The area of each triangle is computed using its base and height.

What is the significance of the apothem of the pyramid?

The apothem of the pyramid is crucial for calculating the height of the triangular faces, which helps in determining the lateral area of the pyramid.

How can you find the area of a triangle in the pyramid?

To find the area of a triangle, you multiply the base by the height of the triangle and divide by 2. In the case of the pyramid, the base of the triangle is the side length of the pyramid's base, and the height is the slant height or apothem of the pyramid.

What method is used to find the side length of the square base when the diagonal is given?

To find the side length of a square base when the diagonal is given, you use the relationship between the side length (L) and the diagonal (d) of a square: d = L√2. By dividing the diagonal by √2, you can find the side length.

How does the Pythagorean theorem help in solving problems related to pyramids?

The Pythagorean theorem is used to relate the height, the apothem, and the lateral edge of the pyramid. By applying this theorem to the relevant right triangles, you can solve for unknown dimensions such as the height of the triangular faces or the lateral edge.

What is the total area of the pyramid in the example, and how was it calculated?

In the example, the total area of the pyramid was found by first calculating the area of the base (576 cm²) and the lateral area (960 cm²). The total area is the sum of these two values, which gives 1,536 cm².