SIFAT-SIFAT DARI LAYANG-LAYANG & TRAPESIUM [+CONTOH SOAL] KELAS 7 SMP/MTs I THE CODE CHANNEL

Summary

This educational video delves into the properties of geometric shapes, focusing on kites and trapezoids, particularly for a 7th-grade audience. It covers the key properties of kites, including their diagonals, symmetry, and angles, as well as the formula for calculating their area. The video then shifts to trapezoids, discussing their different types, properties, and how to calculate their area using the appropriate formula. The presenter uses examples to clarify these concepts, providing step-by-step solutions to geometry problems, making the content accessible and engaging for students learning these shapes.

Takeaways

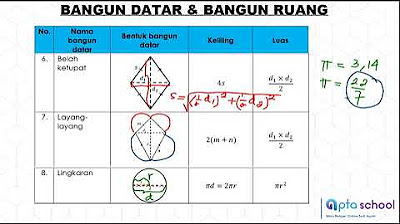
• 😀 Rhombus is a quadrilateral with two pairs of equal sides, and its area is calculated as half the product of the diagonals.
• 😀 A rhombus has two pairs of equal angles, with opposite angles being equal and adjacent angles being supplementary.
• 😀 The diagonals of a rhombus intersect at right angles and bisect each other.
• 😀 The perimeter of a rhombus is the sum of all four sides, and the length of the diagonals is crucial for calculating its area.
• 😀 In a right triangle formed by the diagonals of a rhombus, the Pythagorean theorem can be used to find missing lengths.
• 😀 A trapezoid is a quadrilateral with one pair of parallel sides, known as the bases, and the non-parallel sides are called legs.
• 😀 The sum of the interior angles of a trapezoid is 360 degrees, and the angles between the parallel sides are supplementary.
• 😀 The area of a trapezoid can be calculated using the formula: Area = 1/2 × (sum of the lengths of the parallel sides) × height.
• 😀 Trapezoids can be classified into types, including irregular, right, and isosceles trapezoids.
• 😀 A right trapezoid has a right angle, and isosceles trapezoid has equal non-parallel sides, often simplifying the calculation of height.

Q & A

What are the main properties of a kite as discussed in the video?

A kite has four sides with two pairs of equal-length sides. Its diagonals intersect at right angles and are of unequal lengths. The kite also has two pairs of equal angles, with one pair being congruent (e.g., angle A equals angle C), and it has one axis of symmetry.

How is the area of a kite calculated?

The area of a kite is calculated using the formula: Area = 1/2 × Diagonal 1 × Diagonal 2.

What is the significance of the Pythagorean theorem in calculating the dimensions of a kite?

The Pythagorean theorem is used to find the lengths of the diagonals in a kite, as the diagonals intersect at right angles, forming right triangles. The theorem helps calculate the missing sides of these triangles.

What are the types of trapezoids mentioned in the video?

The video mentions three types of trapezoids: irregular trapezoids, right trapezoids (which have one right angle), and isosceles trapezoids (where the non-parallel sides are of equal length).

What is the formula for the area of a trapezoid?

The area of a trapezoid is calculated using the formula: Area = 1/2 × (Base 1 + Base 2) × Height.

How do the angles in a trapezoid relate to each other?

In a trapezoid, the sum of the angles between the two parallel sides equals 180°. For example, angle A + angle B = 180°, and angle C + angle D = 180°.

What is the main characteristic of the diagonals in a kite?

The diagonals of a kite intersect at right angles (90°) but are not of equal length.

What are the properties of the sides and angles of a trapezoid?

A trapezoid has one pair of opposite sides that are parallel, and the sum of the angles between the parallel sides is always 180°.

How can you calculate the height of a trapezoid using the Pythagorean theorem?

To calculate the height of a trapezoid using the Pythagorean theorem, you can create a right triangle by splitting the trapezoid and use the theorem to find the missing side that represents the height.

What are the steps to calculate the area of a right trapezoid as shown in the video?

To calculate the area of a right trapezoid, first identify the lengths of the parallel sides (Base 1 and Base 2) and the height. Then use the formula: Area = 1/2 × (Base 1 + Base 2) × Height.