Movimientos circulares, MCU y MCUA - rápido y fácil

Summary

In this video, Antonio explains the fundamentals of circular motion, focusing on the use of angular measurements like angle, angular velocity, and angular acceleration instead of linear ones. He covers key topics like uniform circular motion, angular acceleration, and unit conversions between revolutions per minute and radians per second. Antonio also clarifies the importance of the period and frequency in circular motion, drawing comparisons with linear motion. The video emphasizes practical application through formulas, aiming to make the understanding and problem-solving of circular motion easier for students.

Takeaways

• 😀 The video focuses on circular motion, using examples like the Earth's orbit around the Sun and a carousel ride.
• 😀 In circular motion, angular quantities (angle, angular velocity, angular acceleration) are more useful than linear quantities like distance and speed.
• 😀 The angle swept by an object in circular motion is measured in radians, with 2π radians representing one full revolution.
• 😀 It's essential to set your calculator to radians when calculating angular measurements, as default settings often use degrees.
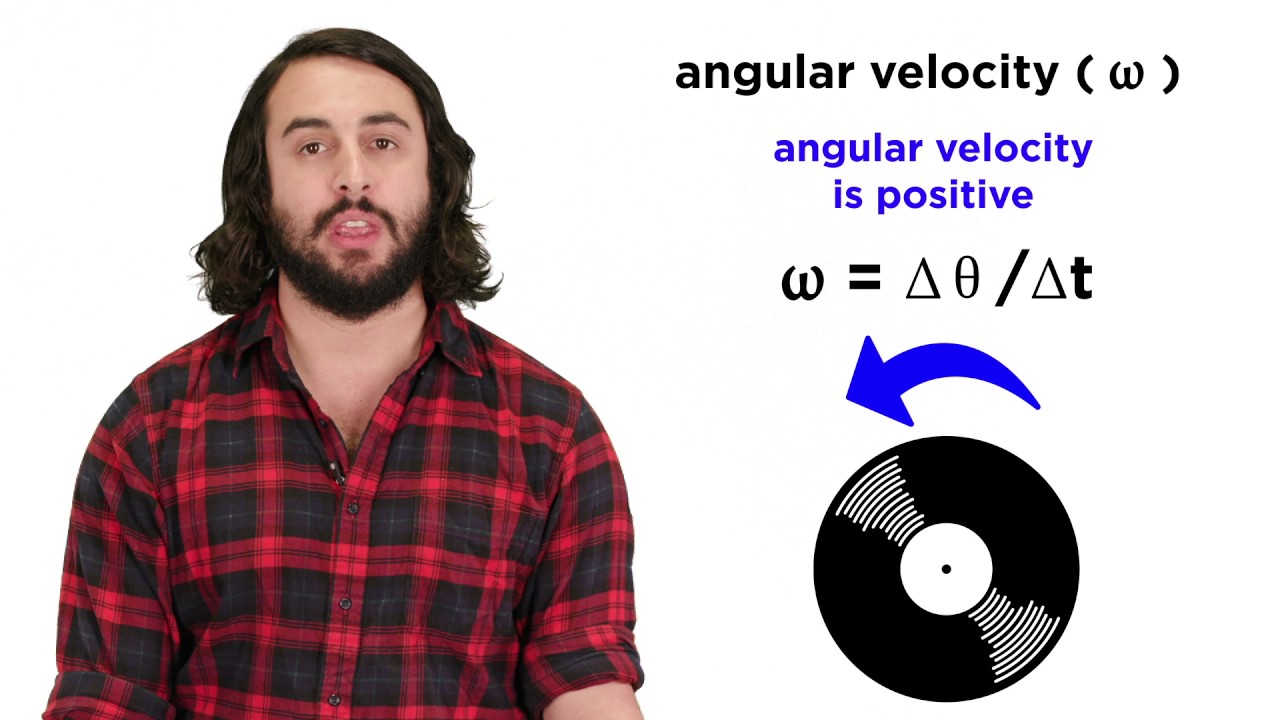
• 😀 The angular position (θ), angular velocity (ω), and angular acceleration (α) are the key parameters for studying circular motion.
• 😀 In uniform circular motion (UCM), the angular velocity remains constant, and the acceleration is purely normal (perpendicular to velocity).
• 😀 The normal acceleration in UCM is given by the equation aₙ = ω² * r, where ω is the angular velocity and r is the radius.
• 😀 The period (T) is the time it takes to complete one full revolution, and the frequency (f) is the number of revolutions per second. These are inversely related.
• 😀 Angular velocity and frequency are connected: ω = 2π * f, where f is the frequency in hertz (Hz).
• 😀 In uniformly accelerated circular motion, the equations are similar to those in linear motion, but with angular quantities: θ = θ₀ + ω₀ * t + ½ * α * t².
• 😀 Students often struggle with converting units in exercises, such as converting revolutions per minute to angular velocity in radians per second, but the process is straightforward.

Q & A

What is the main focus of the video?

The main focus of the video is on circular motion, explaining its principles and how to study it using angular quantities instead of linear ones.

Why is it easier to use angular quantities when studying circular motion?

It is easier to use angular quantities because they simplify the study of circular motion. Instead of dealing with linear magnitudes like position, velocity, and acceleration, we can use angular displacement, angular velocity, and angular acceleration.

What is the relationship between degrees and radians in circular motion?

In circular motion, 2π radians equal 360 degrees, meaning a full circle corresponds to 2π radians. This conversion is essential when calculating angular displacement.

How is angular velocity measured?

Angular velocity is measured in radians per second (rad/s) and represents the rate at which the angle changes with respect to time.

What is the difference between angular acceleration and linear acceleration?

Angular acceleration refers to the rate of change of angular velocity with respect to time, measured in rad/s², while linear acceleration is the rate of change of velocity with respect to time, measured in meters per second squared.

What are the two components of acceleration in circular motion?

The two components of acceleration in circular motion are the normal (centripetal) acceleration, which is responsible for changing the direction of velocity, and the tangential acceleration, which affects the magnitude of the velocity.

What is uniform circular motion (UCM), and how is it different from linear motion?

Uniform circular motion (UCM) occurs when an object moves around a circle at a constant angular velocity. It is similar to uniform linear motion but describes motion along a circular path instead of a straight line.

How do you calculate the normal acceleration in uniform circular motion?

The normal acceleration, or centripetal acceleration, can be calculated using the formula aₙ = ω²r, where ω is the angular velocity and r is the radius of the circular path.

What is the period of circular motion, and how is it related to frequency?

The period of circular motion is the time it takes for an object to complete one full revolution. It is inversely related to the frequency, where frequency (f) is the number of revolutions per second, and the period (T) is the inverse of the frequency: T = 1/f.

How do you convert revolutions per minute (RPM) into angular velocity in radians per second?

To convert revolutions per minute (RPM) to angular velocity in radians per second, you multiply the RPM by 2π and divide by 60. For example, 10 RPM equals (10 × 2π) / 60 = π/3 radians per second.