Deriving Torricelli's Theorem using Bernoulli's Equation
Summary
TLDRIn this video, the concept of Torricelli's Theorem is explored, a special case of Bernoulli’s equation, named after Evangelista Torricelli, an Italian physicist and mathematician. The video explains the flow of an ideal fluid from a large reservoir through a small spigot, deriving the equation for the speed of the fluid using Bernoulli’s principles. The connection to gravitational potential energy is also discussed, showing how the speed of a fluid flowing out of the spigot mirrors the speed of a ball dropped from the same height. This surprising realization, discovered centuries ago, highlights the beauty of fluid dynamics and energy conservation.
Takeaways
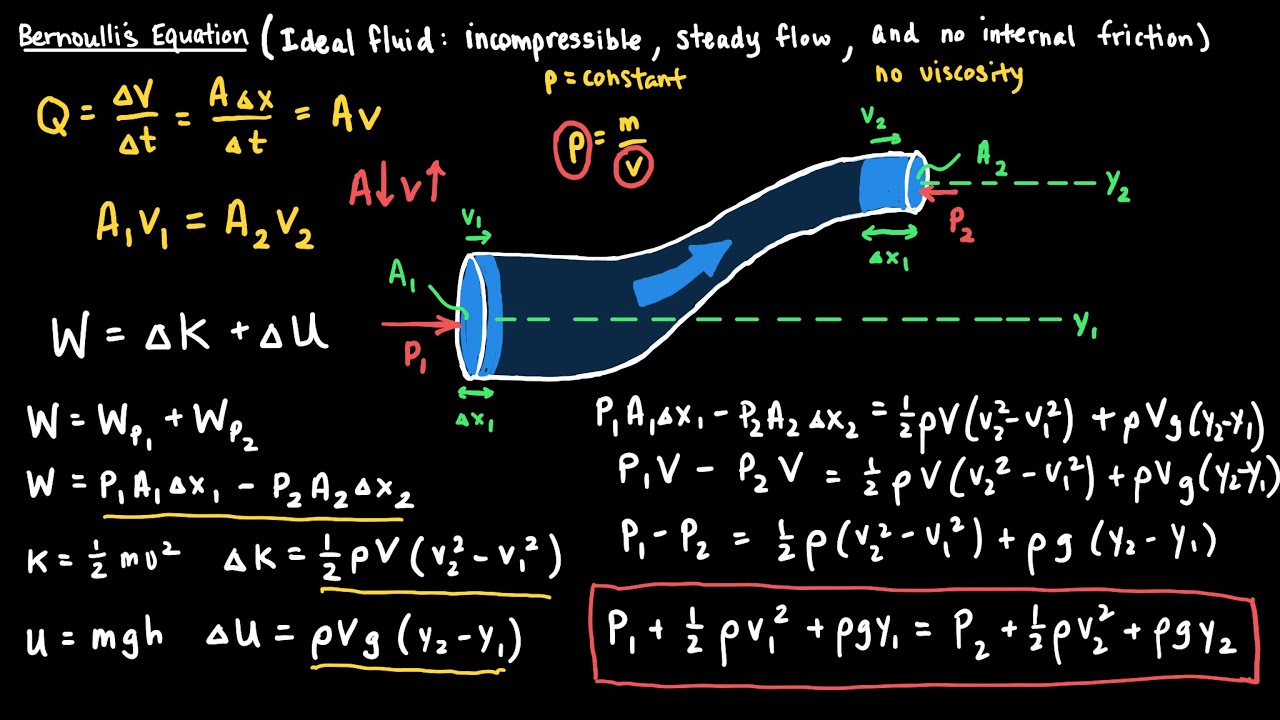
- 😀 Bernoulli's equation is used to describe the relationship between fluid speed, pressure, and height in a system.
- 😀 Torricelli's Theorem is a special case of Bernoulli's equation, derived to calculate the speed of fluid exiting a small spigot in a large reservoir.
- 😀 Evangelista Torricelli, an Italian physicist and student of Galileo, discovered Torricelli's Theorem nearly a century before Bernoulli.
- 😀 The ideal fluid assumption and the large reservoir size make the fluid speed at point 1 (top of the reservoir) almost zero.
- 😀 The pressure at points 1 and 2 in the system are both equal to atmospheric pressure, allowing them to cancel out in the equation.
- 😀 The small spigot causes a negligible pressure difference between the top of the reservoir and the spigot, due to the density difference between air and water.
- 😀 The vertical height of point 2 is zero, simplifying the equation further by eliminating the height term for point 2.
- 😀 Torricelli’s Theorem states that the speed of fluid exiting the spigot equals the square root of 2 times the gravitational field strength times the height at point 1.
- 😀 The speed of a ball falling from the height of point 1 to point 2 can be derived using mechanical energy conservation, resulting in the same speed as the fluid exiting the spigot.
- 😀 The speed of the ball and the fluid are identical when the vertical height difference is the same, showing the connection between fluid dynamics and gravitational motion.
- 😀 This scientific understanding, discovered over 400 years ago, was a groundbreaking realization in fluid dynamics and physics.
Q & A
What is Bernoulli’s equation used for in fluid dynamics?
-Bernoulli’s equation is used to describe the relationship between the pressure, velocity, and elevation of a fluid in motion. It can be applied to determine the speed of fluid flow, such as in the case of a fluid exiting a spigot from a large reservoir.
Who discovered Torricelli’s Theorem and what is its significance?
-Torricelli’s Theorem was discovered by Evangelista Torricelli, an Italian physicist and mathematician, and a student of Galileo. The theorem is a special case of Bernoulli’s equation and provides a way to calculate the speed of fluid flowing out of a spigot from a large reservoir.
What is the key assumption made when applying Torricelli’s Theorem to a large reservoir?
-The key assumption is that the fluid speed at the top of the reservoir (point 1) is approximately zero because the cross-sectional area at this point is very large compared to the spigot’s small cross-sectional area. Additionally, the height of the fluid in the reservoir does not significantly change as the fluid flows out.
What simplifications are made when deriving Torricelli’s Theorem from Bernoulli’s equation?
-When deriving Torricelli’s Theorem, several simplifications are made, including: both points 1 and 2 (top of the reservoir and spigot) are exposed to atmospheric pressure and cancel out, the speed at point 1 is negligible, and the vertical height at point 2 is zero.
How is the speed of fluid flowing out of the spigot derived using Bernoulli’s equation?
-By applying Bernoulli’s equation, we simplify it to: fluid density times gravitational field strength times height at point 1 equals one-half times fluid density times the square of speed at point 2. Solving for speed at point 2 results in the equation: speed at point 2 equals the square root of 2 times gravitational field strength times height 1.
How does Torricelli’s Theorem relate to the mechanics of a freely falling ball?
-Torricelli’s Theorem can be derived by comparing the speed of fluid flowing out of a spigot to the speed of a ball freely falling from the same height. The mechanical energy of the ball remains constant, and by applying this concept, the speed of the ball at the spigot is found to be equal to the speed of the fluid flowing out.
What types of energy are considered when analyzing the falling ball in relation to Torricelli’s Theorem?
-When analyzing the falling ball, the system’s mechanical energy consists of gravitational potential energy at point 1 (height h1) and kinetic energy at point 2 (speed at point 2). The conservation of mechanical energy principle is used to equate these energies and solve for the ball’s speed at point 2.
How is mechanical energy conserved when a ball falls from point 1 to point 2?
-Mechanical energy is conserved because the gravitational potential energy of the ball at point 1 is converted into kinetic energy as the ball falls to point 2. The total mechanical energy remains the same throughout the fall, allowing us to calculate the speed at point 2 using the relationship between the two forms of energy.
What is the significance of the equation for the speed of the ball and the fluid?
-The equation for the speed of the ball and the fluid—speed equals the square root of 2 times gravitational field strength times height—demonstrates that both the fluid flowing out of the spigot and the falling ball reach the same speed when falling from the same height, despite being different physical processes.
What is the historical significance of Torricelli’s Theorem?
-Torricelli’s Theorem, discovered nearly 400 years ago, was an important advancement in fluid dynamics, providing a method to calculate the speed of fluid flowing from a spigot, which would later be understood as a practical application of Bernoulli’s equation.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

The history of the barometer (and how it works) - Asaf Bar-Yosef

Bernoulli's Principle Derivation
Bernoulli's Equation for Fluid Flow Video in Physics

Fluida Dinamis - Konsep Bernoulli - Simple Konsep - Fisika Kelas 11

The story of Mathematics: Emmy Noether
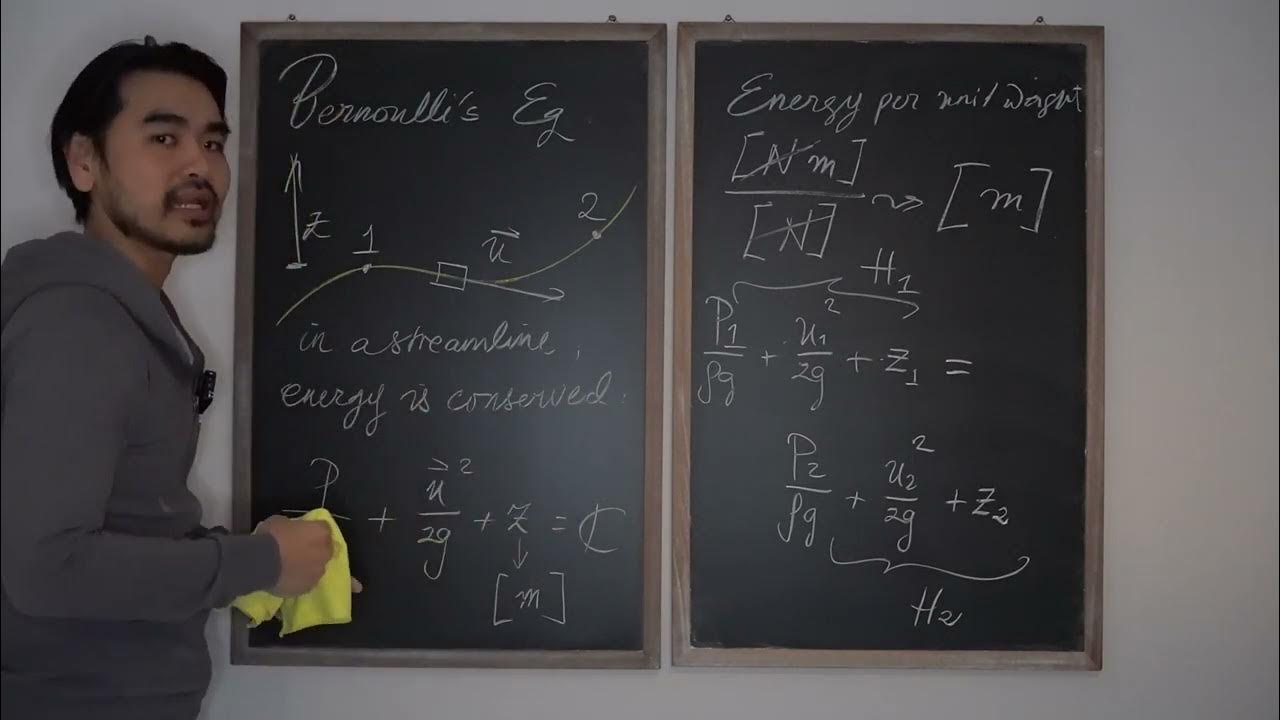
Mekanika Fluida FM01 (Lecture3: 1/8). Persamaan Bernoulli (Pengenalan)
5.0 / 5 (0 votes)