What Is Linear Quadratic Regulator (LQR) Optimal Control? | State Space, Part 4

Summary

This video introduces the concept of Linear Quadratic Regulator (LQR) control, explaining its role as an optimal control technique using state space representation. It contrasts LQR with pole placement control, emphasizing that while both use state feedback, LQR optimizes performance and actuator effort through a cost function. The video illustrates how LQR balances these factors by adjusting weighting matrices (Q and R), offering practical examples in MATLAB. It highlights the flexibility of LQR in tuning system behavior and optimizing control performance, making it an accessible and powerful tool for control system design.

Takeaways

• 😀 LQR is a method of optimal control based on state-space representation, aiming to minimize a cost function that balances performance and control effort.
• 😀 The structure of LQR and pole placement controllers is similar, both using full-state feedback, but they differ in how the gain matrix K is determined.
• 😀 In pole placement, the gain matrix K is derived by choosing specific pole locations, which can be challenging for complex systems.
• 😀 LQR avoids choosing pole locations directly, instead focusing on a cost function that minimizes performance and control effort by adjusting matrices Q and R.
• 😀 The cost function in LQR penalizes state error (performance) and actuator effort (control effort) to balance system behavior.
• 😀 Performance is measured by how quickly the system’s states return to the desired equilibrium, with larger state errors penalized more heavily.
• 😀 The R matrix in LQR controls the amount of actuator effort, and its value is adjusted to balance control effort and system performance.
• 😀 LQR provides an optimal solution by adjusting the weights in the Q and R matrices based on system priorities, such as minimizing time or energy consumption.
• 😀 MATLAB simplifies LQR implementation, allowing designers to adjust Q and R matrices and run simulations to observe system behavior and optimize control.
• 😀 LQR can be more intuitive than pole placement for certain systems, especially when dealing with actuator saturation, as it directly adjusts control effort through the R matrix.

Q & A

What is the primary difference between LQR and pole placement control?

The primary difference is that LQR focuses on optimizing the gain matrix (K) by balancing performance and actuator effort, while pole placement directly places closed-loop poles based on desired system behavior. LQR does not choose specific pole locations but rather aims to minimize a cost function involving both system performance and actuator effort.

Why is it difficult to choose good pole locations in pole placement control for high-order systems?

For high-order systems, selecting the optimal location for poles can become non-intuitive, especially when the system has multiple actuators and complex dynamics. This makes pole placement harder to implement and optimize effectively compared to LQR.

How does LQR determine the optimal gain matrix (K)?

LQR calculates the optimal gain matrix (K) by solving a quadratic optimization problem, which minimizes a cost function that balances performance (how quickly the system returns to equilibrium) and actuator effort (the energy or input required to achieve the desired performance).

What are the two main components of the LQR cost function?

The two main components of the LQR cost function are the Q matrix, which penalizes state error (performance), and the R matrix, which penalizes actuator effort (energy usage). These matrices are weighted based on how important each factor is for the specific control problem.

How does the Q matrix affect LQR control?

The Q matrix in LQR affects the performance of the system by penalizing deviations from the desired state. Larger values in Q correspond to a higher penalty for errors in specific states, which makes the system prioritize reducing these errors.

What is the role of the R matrix in LQR control?

The R matrix penalizes actuator effort or energy usage in LQR control. Larger values in R increase the cost of using certain actuators, which encourages the system to use less energy or effort while achieving the desired performance.

Can you use LQR to optimize for both time and energy usage simultaneously? How?

Yes, LQR can optimize for both time and energy usage by adjusting the relative weights in the Q and R matrices. For example, if minimizing time is more important, the Q matrix can be weighted more heavily, while if saving energy is a priority, the R matrix can be adjusted to penalize actuator effort more.

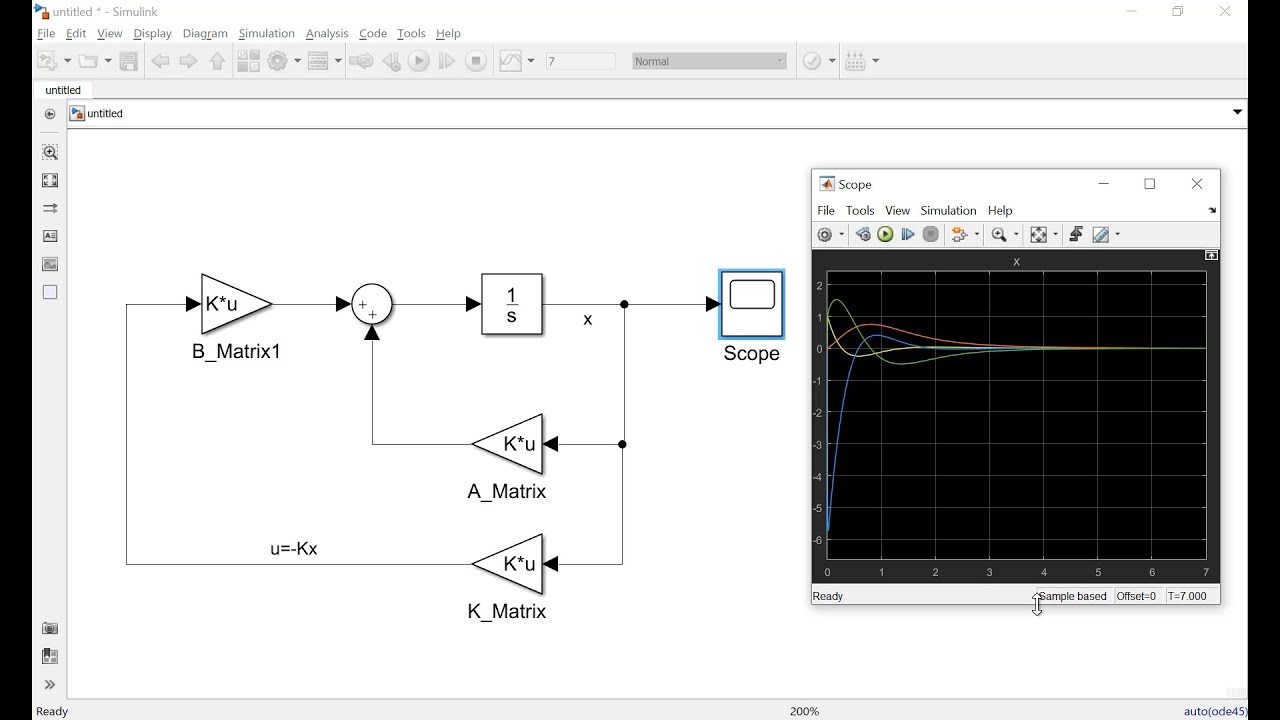
What does the MATLAB example with the rotating mass system demonstrate?

The MATLAB example with the rotating mass system demonstrates how the LQR controller can be tuned by adjusting the Q and R matrices. It shows how different values in these matrices affect the system's performance, such as the time it takes to complete a maneuver and the fuel (energy) consumed.

Why does LQR provide more flexibility compared to pole placement in handling actuator limitations?

LQR provides more flexibility because it directly adjusts the cost function, which includes a penalty for actuator effort. This allows for intuitive tuning of actuator usage and system performance, while pole placement requires specific adjustments to pole locations, which can be difficult to correlate with actuator limitations.

What is the significance of quadratic functions in LQR control?

Quadratic functions are significant in LQR control because they are convex and have a definite minimum value. By using quadratic functions for performance and effort, the system can always find an optimal solution with a clear minimum cost, ensuring stable and efficient control.