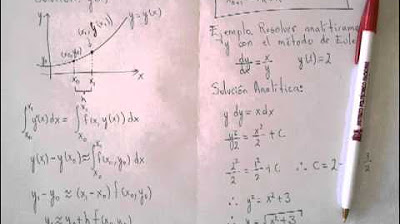MÉTODO EULER MEJORADO

MIZAEL TORRES

9 Dec 201413:58

Summary

TLDREn este tutorial de YouTube, se explica el método de Euler mejorado para resolver problemas de ecuaciones diferenciales. Se presenta un ejemplo práctico con una función dada, donde se utiliza el paso de 0.1 y se demuestra el proceso paso a paso, desde la inicialización hasta el cálculo de valores sucesivos. Se comparan los resultados obtenidos con el método de Euler clásico y se sugiere que el método mejorado ofrece mayor precisión. Además, se menciona la posibilidad de graficar los resultados para una mejor comprensión visual y se hace una llamada a la acción para seguir explorando estos temas en futuros videos.

Takeaways

📚 El vídeo tutorial trata sobre el método de Euler mejorado, una técnica para resolver problemas de ecuaciones diferenciales.
🔍 Se utiliza el método de Euler mejorado para calcular la evolución de una función dada un paso y un límite específicos.
📘 Se presenta un problema específico con una función 'f(x)', un límite de 'a' y un paso 'h', donde 'a1' es igual a 1 y el paso es 0.1.
📝 Se muestra la fórmula del método de Euler mejorado, que incluye una corrección para mejorar la precisión del cálculo.
🔢 Se detalla el proceso de cálculo paso a paso, desde la inicialización de variables hasta la aplicación de la fórmula para obtener valores de 'y'.
📉 Se comparan los resultados obtenidos con el método de Euler mejorado con los resultados teóricos, destacando la mejora en la precisión.
📈 Se menciona la necesidad de graficar los resultados para una mejor comprensión visual de los datos.
🖥️ Se discute la implementación del método en un programa, incluyendo la llamada a funciones y la manipulación de variables.
👨‍🏫 El tutorial incluye una explicación de cómo corregir errores y cómo ajustar los parámetros para obtener los resultados deseados.
📊 Se grafica la función y se compara con otros métodos como el de Taylor, destacando la superioridad del método de Euler mejorado en términos de precisión.
👋 El presentador deseospor un vídeo instructivo y esperanzado que haya sido útil para los espectadores.

Q & A

¿Qué es el método de Euler mejorado y cómo se utiliza en el video?
-El método de Euler mejorado es una técnica numérica para resolver ecuaciones diferenciales de orden uno. En el video, se utiliza para resolver un problema específico, tomando dos aproximaciones sucesivas para mejorar la precisión en el cálculo de la función.
¿Cuál es la función y los límites utilizados en el ejemplo del video?
-La función utilizada en el ejemplo es 'f(x, y) = x', con 'a' igual a 1.5 como el límite superior y 'a1' igual a 1 como el límite inferior, y un paso 'h' de 0.1.
¿Cómo se describe la fórmula del método de Euler mejorado en el script?
-La fórmula del método de Euler mejorado se describe como 'y_n+1 = y_n + h*(f(x_n, y_n) + f(x_n+h, y_n+h))/2', donde 'y_n' es la aproximación del valor de 'y' en el punto 'x_n'.
¿Qué es el primer paso para resolver el problema utilizando el método de Euler mejorado según el video?
-El primer paso es resolver la segunda ecuación, que es 'y_n+1 = y_n + h*f(x_n, y_n)/2', para obtener una aproximación inicial de 'y_n+1'.
¿Cómo se calcula el valor de 'y2' en el ejemplo del video?
-Para calcular 'y2', se utiliza la fórmula 'y_n+1 = y_n + h*f(x_n, y_n)/2', sustituyendo 'y1' con '1 + 0.1*2*1.1', lo que resulta en '1.2'.
¿Cuál es la diferencia entre el método de Euler y el método de Euler mejorado?
-El método de Euler mejorado ofrece una mejor aproximación al valor real de la función en comparación con el método de Euler estándar, ya que utiliza una combinación de las derivadas en dos puntos consecutivos para reducir el error.
¿Cómo se compara el resultado del método de Euler mejorado con otros métodos numéricos en el video?
-El video compara los resultados obtenidos con el método de Euler mejorado con los resultados de otros métodos numéricos, como el método de Taylor, para demostrar la mayor precisión del método de Euler mejorado.
¿Qué se hace para graficar los resultados en el video?
-Para graficar los resultados, se utiliza un bloque de código que incluye la función a graficar, los parámetros de inicio y fin, y una opción para agregar cuadrícula a la gráfica.
¿Qué se debe hacer si se encuentra un error al ejecutar el código de graficación en el video?
-Si se encuentra un error al ejecutar el código de graficación, se debe revisar si todas las funciones y variables están definidas correctamente y si los parámetros están configurados adecuadamente.
¿Cómo se resuelve el problema de la gráfica que no se muestra correctamente en el video?
-Para resolver el problema de la gráfica que no se muestra correctamente, se sugiere guardar los valores intermedios y revisar si hay un error en la forma en que se están calculando o almacenando estos valores.
¿Qué se aprende al final del video sobre la comparación de los métodos numéricos?
-Al final del video, se aprende que el método de Euler mejorado ofrece una mayor precisión en los cálculos en comparación con el método de Euler estándar y otros métodos, lo que lo hace más útil para resolver problemas de ecuaciones diferenciales.

Outlines

00:00

📚 Introducción al Método de Euler Mejorado

El primer párrafo presenta un tutorial sobre el Método de Euler Mejorado, una técnica numérica para resolver problemas de ecuaciones diferenciales. Se describe el problema de resolver una función dada, donde ya es igual a 1.5, con un paso de 0.1 y utilizando la fórmula de Euler Mejorado. Se menciona la necesidad de resolver dos ecuaciones para calcular el valor de la función en un nuevo punto, y se muestran los pasos iniciales para calcular g1, g2, g3, etc., hasta llegar a los valores deseados.

05:01

🔍 Continuación del Cálculo y Ejemplo Práctico

Este párrafo continúa el proceso de cálculo utilizando el Método de Euler Mejorado. Se describe cómo se ejecuta un programa con un ciclo para calcular los valores de g1, g2, g3, g4 y g5, obteniendo resultados con cuatro decimales de precisión. Se menciona la importancia de la función y cómo se puede graficar la función xy para visualizar los resultados. También se discuten los errores que pueden ocurrir si no se llama a la función correcta y cómo corregirlos, así como la importancia de los parámetros para la precisión del cálculo.

10:04

📊 Graficación de Resultados y Comparación con Otros Métodos

El tercer párrafo se enfoca en la graficación de los resultados obtenidos con el Método de Euler Mejorado. Se describe el proceso de eliminación de resultados numéricos para centrarse en la gráfica, y se mencionan los errores que pueden ocurrir si no se guarda la información adecuadamente. Se muestra cómo se grafica la función y cómo se comparan los resultados con los obtenidos en ejercicios previos. Además, se discute la precisión del Método de Euler Mejorado en comparación con otros métodos numéricos y se concluye con una esperanza de que el contenido del video haya sido útil y agradable para los espectadores.

Mindmap

Keywords

💡Euler mejorado

El método de Euler mejorado es un tema central en el video y se refiere a una técnica matemática para resolver problemas de ecuaciones diferenciales ordinarias. Es una mejora del método de Euler estándar, que proporciona una mayor precisión en los resultados. En el script, se utiliza este método para resolver un problema específico, mostrando los pasos para calcular los valores de 'y' en diferentes puntos de 'x', lo que ilustra su importancia en el tema del video.

💡ecuaciones

Las ecuaciones diferenciales son una parte fundamental del contenido del video, ya que el método de Euler mejorado se aplica para resolverlas. En el contexto del video, se menciona una ecuación diferencial que involucra la función 'f(x, y)', y se resuelve utilizando el método de Euler mejorado. Las ecuaciones son esenciales en matemáticas y física para modelar cambios y relaciones entre variables.

💡función

En el video, la función se refiere a una relación matemática que asigna un valor de 'y' a cada valor de 'x' en el dominio de la ecuación diferencial. La función 'f(x, y)' es clave en el proceso de aplicar el método de Euler mejorado, como se muestra en el script donde se calcula 'y1' a partir de 'y0' y el paso 'h'. La función es central para entender cómo se modelan y resuelven las ecuaciones en el video.

💡paso

El 'paso' es un término utilizado para describir el intervalo o diferencia entre los puntos en los que se evalúa la función en el método numérico de Euler mejorado. En el script, el paso 'h' es igual a 0.1, y es un parámetro crucial que afecta la precisión y la resolución de la solución numérica. Un paso más pequeño generalmente aumenta la precisión del resultado, pero también aumenta la cantidad de cálculos necesarios.

💡límite

El 'límite' en el contexto del video se refiere al valor final o al punto más allá del cual se detiene el proceso de iteración en el método de Euler mejorado. En el script, el límite es mencionado como 'a', que es igual a 1.5, y es el punto hasta donde se resuelve la ecuación diferencial. El límite es importante para determinar el rango de los valores que se van a calcular.

💡valor inicial

El 'valor inicial' es el punto de partida para el proceso de iteración en el método numérico. En el script, el valor inicial 'y0' es igual a 1, y es la base desde la cual se calculan los siguientes valores de 'y'. El valor inicial es fundamental para establecer la trayectoria de la solución numérica y es un aspecto clave en la resolución de ecuaciones diferenciales.

💡precisión

La 'precisión' es un concepto importante en el video, ya que el método de Euler mejorado busca mejorar la precisión de las soluciones numéricas en comparación con el método de Euler estándar. El script menciona la precisión como un beneficio del método de Euler mejorado, y se ilustra cómo este método proporciona resultados más precisos que otros métodos numéricos.

💡graficar

El término 'graficar' se refiere a la acción de representar visualmente los datos o funciones en un gráfico. En el video, se menciona la necesidad de graficar la función y los resultados obtenidos con el método de Euler mejorado para una mejor comprensión y análisis visual. La graficación es una herramienta útil para visualizar cómo varía una función y para comparar los resultados de diferentes métodos numéricos.

💡múltiples métodos

El video hace referencia a diferentes métodos numéricos para resolver ecuaciones diferenciales, como el método de Euler mejorado, el método de Euler estándar y el método de Taylor. Estos métodos son comparados en términos de precisión y eficiencia. En el script, se menciona la comparación de los resultados obtenidos con estos métodos, destacando las ventajas del método de Euler mejorado.

💡comentarios

Los 'comentarios' en el contexto del script se refieren a las anotaciones o explicaciones que se incluyen en el código para ayudar a entender su funcionamiento o propósito. En el video, se menciona la importancia de mantener los comentarios en el código, especialmente cuando se trata de graficar los resultados o cuando se realiza una comparación entre diferentes métodos numéricos.

Highlights

Tutorial sobre el método de Euler mejorado para resolver problemas de ecuaciones diferenciales.

Se presenta un problema de ecuación diferencial con la función f(x, y) = x * y, y condiciones iniciales y límites.

Se utiliza la fórmula de Euler mejorado para aproximar la solución de la ecuación diferencial.

Se muestra la sustitución de la segunda ecuación en la fórmula principal para resolver el problema.

Se inicia el proceso de cálculo con la segunda fórmula para determinar y1.

Se calcula el valor de y1 utilizando el paso h = 0.1 y el valor inicial de x0 = 1.

Se describe el proceso para calcular y2, y3, y4 y y5 utilizando el método de Euler mejorado.

Se muestra cómo comparar los resultados obtenidos con el método de Euler mejorado con otros métodos.

Se presenta una función en MATLAB para aplicar el método de Euler mejorado y obtener los resultados.

Se discute la importancia de la precisión y cómo el método de Euler mejorado mejora los resultados.

Se menciona la posibilidad de graficar los resultados para una mejor comprensión visual.

Se proporciona un ejemplo de cómo llamar a la función y establecer los parámetros en MATLAB.

Se explica cómo corregir errores en la ejecución del código en MATLAB.

Se muestra el resultado de los primeros pasos utilizando el método de Euler mejorado.

Se discute la elección del paso y su impacto en la precisión del resultado.

Se presenta la gráfica resultante de los cálculos y cómo se compara con los resultados teóricos.

Se concluye el tutorial con una revisión de los resultados obtenidos y una comparación con otros métodos.