35 DC Tutorial para obtener la solución General de Circuitos RC con Condiciones Iniciales.
Summary
TLDRIn this video, the presenter explores the workings of an RC circuit, where a resistor and capacitor are connected in series with a DC voltage source. The video explains key concepts such as Ohm’s Law, Kirchhoff’s Voltage Law, and the behavior of capacitors in circuits. The presenter provides a step-by-step guide to solving the circuit’s differential equation, showing how to calculate the capacitor's voltage over time. By focusing on a simple and general approach, the video equips viewers with the knowledge to solve various RC circuit problems effectively, using basic principles and clear explanations.
Takeaways
- 😀 An RC circuit consists of a resistor (R) and capacitor (C) connected in series with a DC power supply.
- 😀 Ohm’s Law (voltage = current x resistance) is used to determine the voltage across the resistor in the circuit.
- 😀 Kirchhoff’s Voltage Law (sum of voltages in a closed loop equals zero) is applied to the circuit to relate the voltages across the resistor and capacitor.
- 😀 The current through the capacitor is related to the rate of change of the capacitor's voltage and its capacitance.
- 😀 When a DC voltage is applied to a capacitor, its current is directly proportional to the derivative of the voltage applied.
- 😀 In a steady-state DC circuit, the derivative of a constant voltage applied to a capacitor is zero, meaning the current becomes zero.
- 😀 The initial condition of the capacitor's voltage (V₀) must be considered when solving the circuit, as it may influence the behavior of the circuit.
- 😀 The circuit’s differential equation is derived from applying Kirchhoff’s Voltage Law and the capacitor’s voltage-current relationship.
- 😀 To solve the differential equation, variables are separated, and integration is used to find the voltage across the capacitor over time.
- 😀 The solution to the RC circuit is expressed in the form Vc(t) = V₀ - (V₀ - V) * e^(-t/RC), where V₀ is the initial voltage and V is the input voltage.
- 😀 The constant term in the solution can be determined by applying the initial condition at time t=0, where the voltage across the capacitor is V₀.
Q & A
What is the main focus of the video script?
-The main focus of the video script is explaining how to solve a series RC circuit, where a DC power supply is connected in series with a resistor and a capacitor, and how the voltage across the capacitor behaves over time.
What basic laws of electricity are discussed in the video?
-The video discusses Ohm’s Law, which relates current, voltage, and resistance, and Kirchhoff's Voltage Law, which states that the sum of all voltages in a closed loop must equal zero.
What is Kirchhoff’s Voltage Law and how does it apply to the RC circuit?
-Kirchhoff’s Voltage Law states that the sum of the voltage drops around a closed loop must be zero. In the RC circuit, this law is applied to the source voltage, the voltage across the resistor, and the voltage across the capacitor, resulting in the equation: -V_{entrada} + V_{resistencia} + V_{capacitor} = 0.
How does a capacitor behave when connected to a DC power supply?
-When a capacitor is connected to a DC power supply, its voltage increases over time until it reaches the value of the power supply. The current through the capacitor is initially high and then decreases as the capacitor charges, ultimately reaching zero once the voltage is constant.
Why is the derivative of the voltage important in the capacitor’s equation?
-The derivative of the voltage is important because it describes how the voltage changes over time. Since the current through a capacitor is proportional to the rate of change of the voltage (derivative), it is crucial for determining the behavior of the circuit.
What does the equation I_C = C * dV_C/dt represent?
-The equation I_C = C * dV_C/dt represents the current through the capacitor (I_C) in terms of its capacitance (C) and the rate of change of voltage across the capacitor (dV_C/dt). It is a fundamental equation for capacitor behavior in an electric circuit.
What role does the initial voltage on the capacitor play in solving the circuit?
-The initial voltage on the capacitor, represented as V_s0, plays a critical role in determining the behavior of the capacitor's voltage over time. It provides the starting point for the voltage across the capacitor, which is used to calculate how the voltage evolves as the circuit operates.
What is the general solution for the voltage across the capacitor in an RC circuit?
-The general solution for the voltage across the capacitor in an RC circuit is given by the equation: V_C(t) = V_{entrada} - (V_{entrada} - V_s^0) * e^(-t/(RC)), where V_C(t) is the voltage across the capacitor at time t, V_{entrada} is the input voltage, V_s^0 is the initial voltage on the capacitor, R is the resistance, and C is the capacitance.
How does the resistance and capacitance affect the time it takes for the capacitor to charge?
-The resistance (R) and capacitance (C) determine the time constant (RC), which controls the charging rate of the capacitor. A larger resistance or capacitance results in a longer time constant, causing the capacitor to charge more slowly. Conversely, a smaller resistance or capacitance causes the capacitor to charge more quickly.
What is the significance of the constant k4 in the equation for the capacitor’s voltage?
-The constant k4 represents a term related to the initial conditions of the circuit, specifically the initial voltage across the capacitor at time t = 0. It is determined by the difference between the input voltage and the initial voltage across the capacitor, and it helps define the capacitor’s voltage behavior over time.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

7.6 Step Response pada Rangkaian RC (1 dari 3)
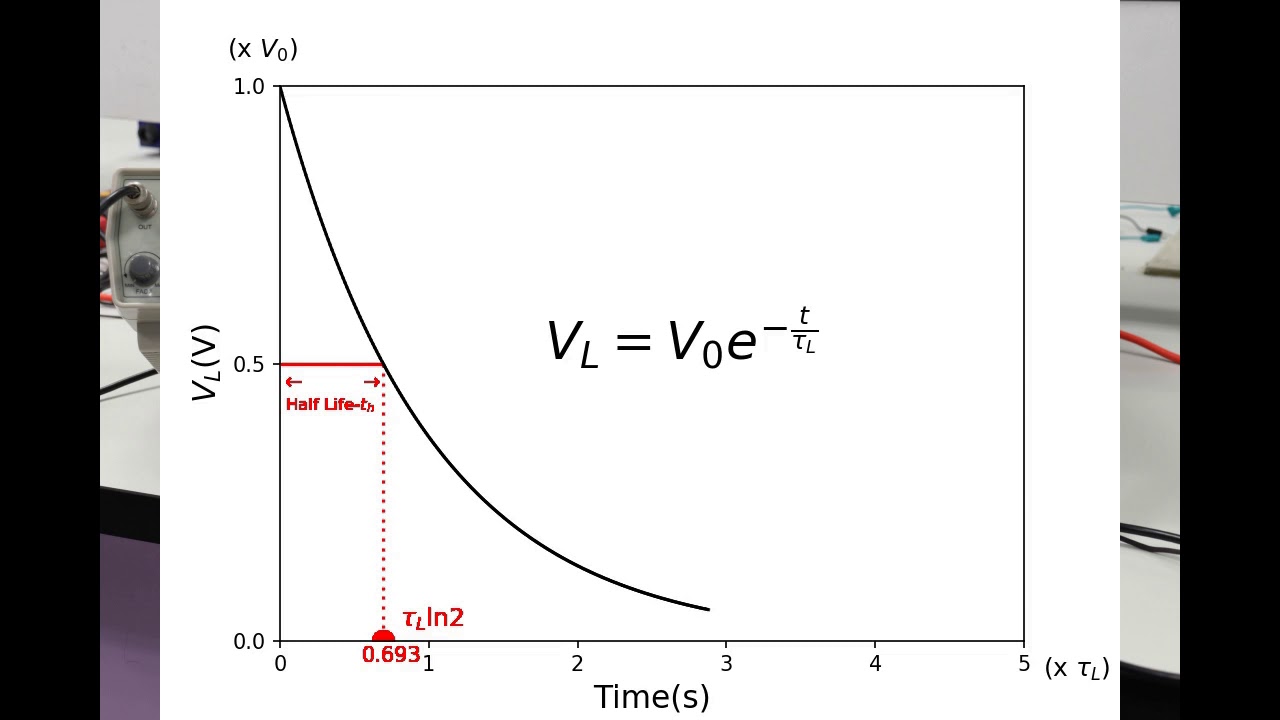
RC and RL Circuits
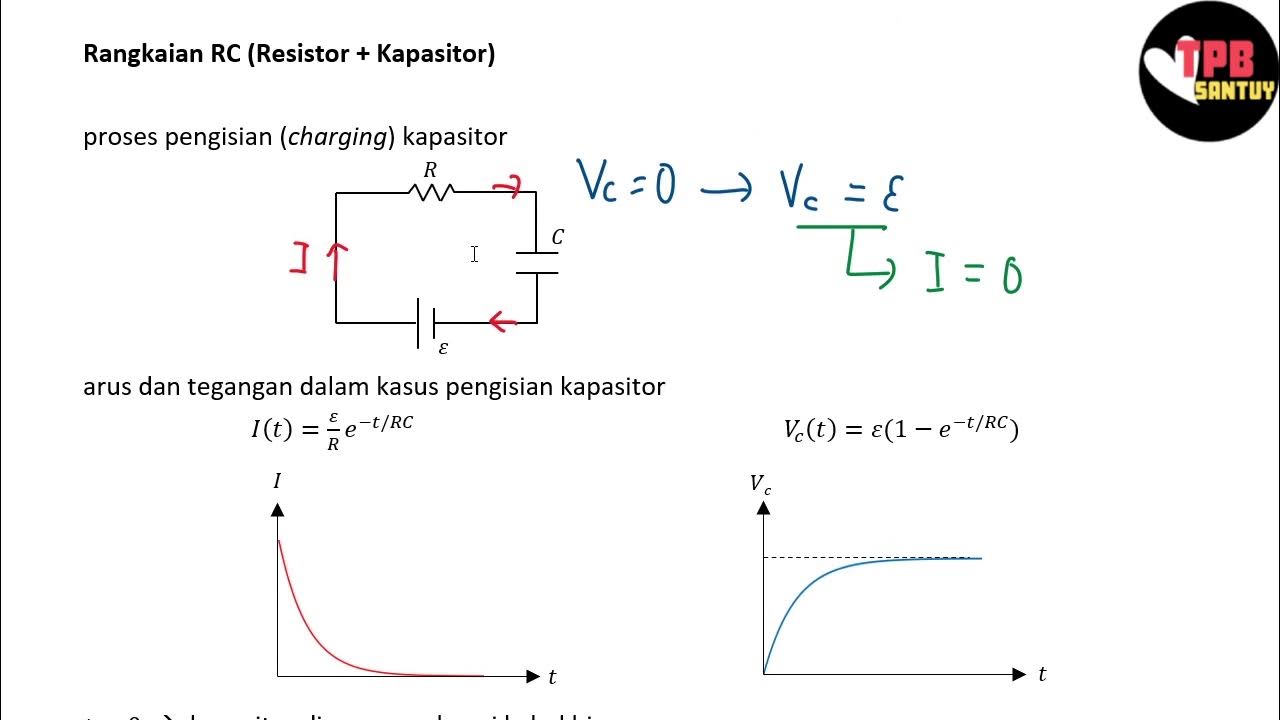
Rangkaian RC (Resistor-Kapasitor) | Rangkaian DC | Part 5 | Fisika Dasar
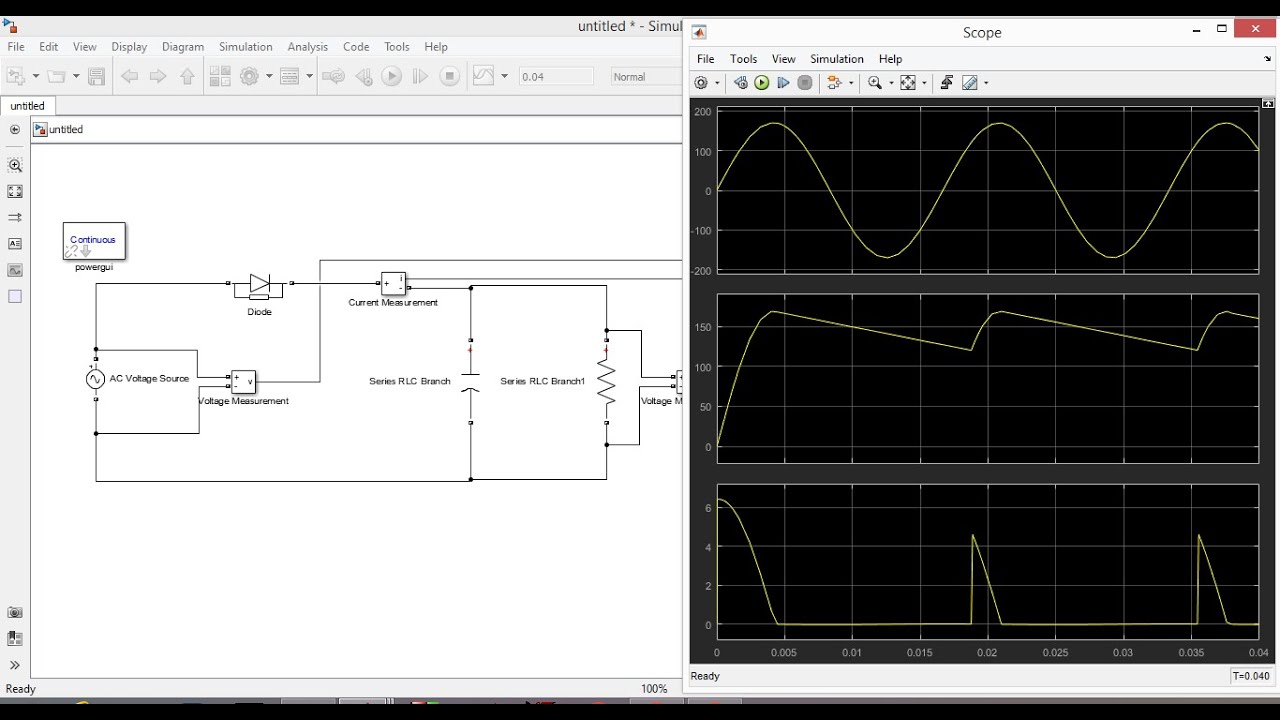
Half Wave Unctrolled Rectifier with C filter Matlab Simulink

Positive & Negative Clamper Circuits

MODUL1 PENYEARAH 1PHASE (HALF WAVE DAN FULL WAVE) MENGGUNAKAN SIMULINK MATLAB
5.0 / 5 (0 votes)