Colisões Elásticas e Inelásticas | Física 1 para Ensino Superior
Summary
TLDRThe video discusses different types of collisions through an example involving two balls. It explains how to calculate the velocity after a collision and identifies the type of collision based on energy and momentum conservation. The collision is partially elastic, as the momentum is conserved but the kinetic energy is not, dropping from 8 J to 5 J. The video also compares inelastic and perfectly elastic collisions, emphasizing how energy loss distinguishes the partially elastic collision. The key takeaway is that in a partially elastic collision, the objects move separately but with a loss of kinetic energy.
Takeaways
- 😀 The problem involves two balls colliding, with one initially moving and the other at rest.
- 😀 The conservation of momentum is used to calculate the velocity of the second ball after the collision.
- 😀 The final velocity of the second ball (V2) after the collision is determined to be 1.5 m/s.
- 😀 The collision cannot be classified as inelastic, as the two balls do not stick together after the collision.
- 😀 The possible collision types are a partially elastic or a perfectly elastic collision.
- 😀 To classify the collision, the system's kinetic energy before and after the collision is compared.
- 😀 Before the collision, the total kinetic energy is 8 J, with only the first ball contributing.
- 😀 After the collision, the total kinetic energy decreases to 5 J, indicating energy loss.
- 😀 Since kinetic energy is not conserved, the collision is classified as partially elastic, not perfectly elastic.
- 😀 In a perfectly elastic collision, both momentum and kinetic energy are conserved, which is not the case here.
- 😀 The narrator compares this collision to inelastic and elastic collisions to explain the loss of kinetic energy.
Q & A
What is the initial kinetic energy of the system before the collision?
-The initial kinetic energy is 8 Joules. This is calculated by using the formula for kinetic energy: KE = 1/2 * m * v^2, where the mass of the moving ball is 4 kg and its velocity is 2 m/s.
How is the velocity of the second ball calculated after the collision?
-The velocity of the second ball is calculated using the principle of conservation of momentum. By setting the total momentum before and after the collision equal, we can solve for the final velocity of the second ball, which is 1.5 m/s.
What type of collision is observed in this scenario?
-This is a partially elastic collision. The momentum of the system is conserved, but the kinetic energy is not fully conserved, as there is a loss of kinetic energy after the collision.
Why is this not a perfectly elastic collision?
-This is not a perfectly elastic collision because the kinetic energy is not conserved. In a perfectly elastic collision, both momentum and kinetic energy are conserved, but in this case, the kinetic energy decreases from 8 J to 5 J.
What is the key difference between an elastic and inelastic collision?
-In an elastic collision, both momentum and kinetic energy are conserved. In contrast, in an inelastic collision, momentum is conserved, but kinetic energy is not, and the objects may stick together after the collision.
What is the final kinetic energy of the system after the collision?
-The final kinetic energy of the system after the collision is 5 Joules. This is calculated by adding the kinetic energy of both balls after the collision.
How do you classify a collision as partially elastic?
-A collision is classified as partially elastic when the momentum of the system is conserved but kinetic energy is not fully conserved. In this case, the total kinetic energy before and after the collision differs, indicating energy loss.
What happens to the two balls after the collision in this example?
-After the collision, the two balls move separately, each with a different velocity. The first ball has a velocity of 1.5 m/s, and the second ball also moves with the same velocity of 1.5 m/s.
What was the mass of each ball in the scenario?
-Each ball has a mass of 4 kg, as stated in the script, which is used in calculating both the initial and final kinetic energy.
Why was the collision not classified as inelastic in this case?
-The collision was not classified as inelastic because the two balls did not stick together after the collision. In an inelastic collision, the objects would move together with the same velocity, but in this case, they moved separately.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Conservation of Momentum | Elastic and Inelastic Collision | Grade 9 Science Quarter 4 Week 4

Introduction to Elastic and Inelastic Collisions

Richard Garriott Space Video Blog: Conservation of Momentum

Distribusi Binomial • Part 12: Contoh Soal Distribusi Peluang Binomial (3)

FISIKA SMA/SMK, TUMBUKAN LENTING SEMPURNA, LENTING SEBAGIAN, TIDAK LENTING SAMA SEKALI
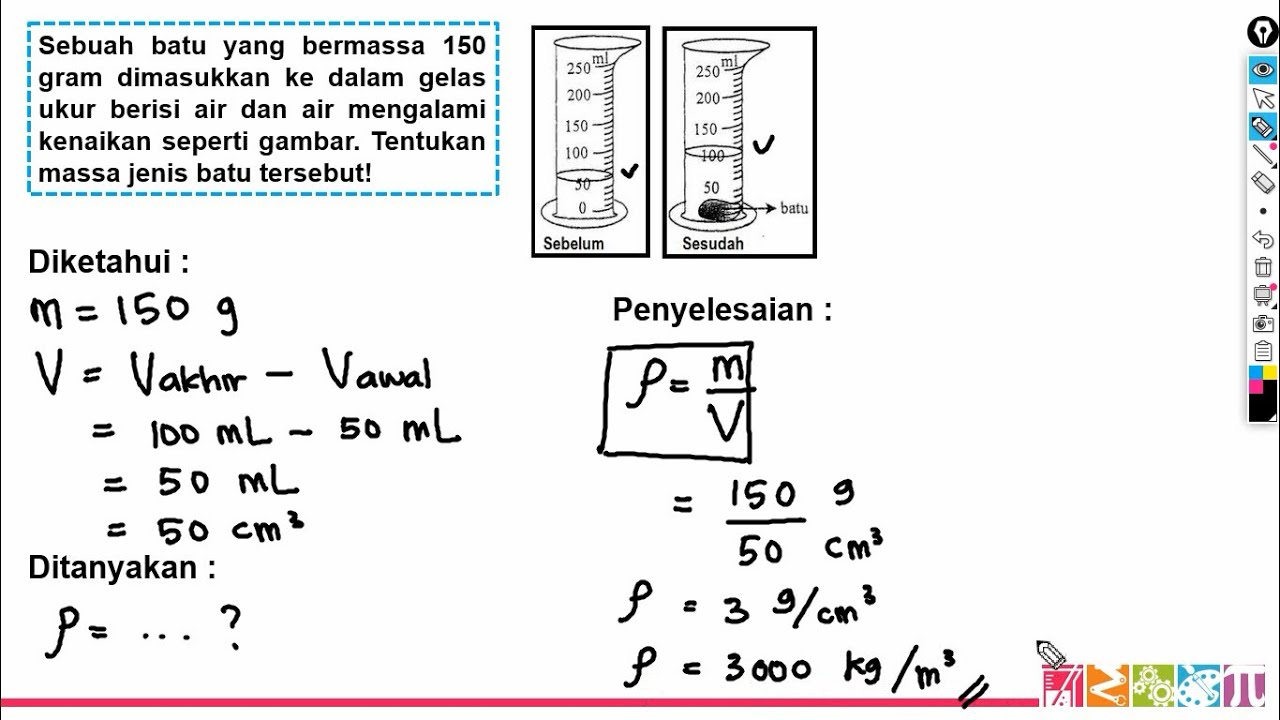
Massa Jenis Benda (IPA SMP)
5.0 / 5 (0 votes)