Geometria Plana: Triângulo Equilátero (Aula 12)

Summary

In this geometry lesson, the instructor covers the topic of equilateral triangles, explaining their properties, formulas for height and area, and providing an in-depth analysis of important concepts like the incribed and circumscribed circles. Key points include the triangle's equal sides and angles, the formula for the height involving √3, and the area formula using side length. The instructor also demonstrates how to apply these concepts through exercises, explaining the relationships between the apothem and radii of the circles inscribed and circumscribed around the triangle. The lesson provides clear explanations and examples to help students better understand these geometrical properties.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What is an equilateral triangle?

An equilateral triangle is a triangle where all three sides are congruent, meaning they have the same length. Additionally, all three angles are also equal, each measuring 60°.

What is the formula for the height of an equilateral triangle?

The formula for the height (h) of an equilateral triangle is h = (l * √3) / 2, where 'l' is the length of the side of the triangle.

How is the area of an equilateral triangle calculated?

The area (A) of an equilateral triangle can be calculated using the formula A = (l² * √3) / 4, where 'l' is the length of a side.

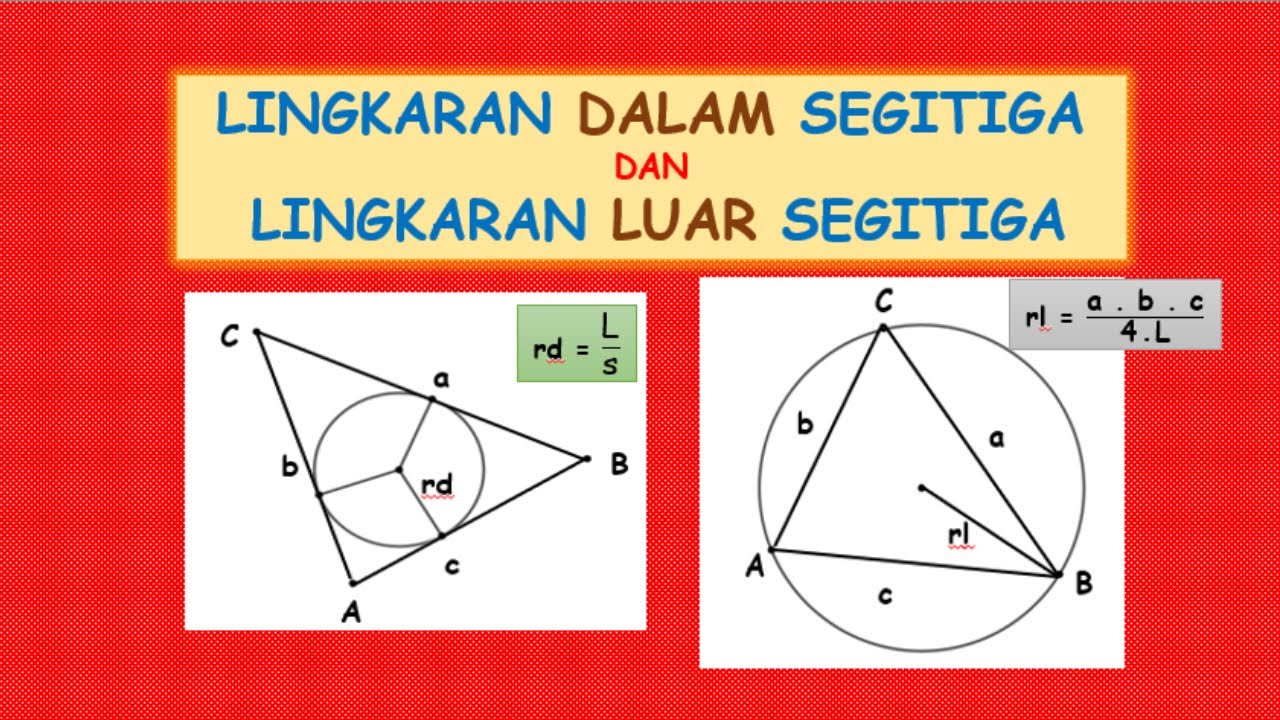
What is the relationship between the apothem and the height of an equilateral triangle?

The apothem (r) of an equilateral triangle is the radius of the inscribed circle. It is always one-third of the height of the triangle, meaning r = h / 3.

How is the radius of the circumcircle of an equilateral triangle related to its height?

The radius (R) of the circumcircle of an equilateral triangle is two-thirds of the height of the triangle, so R = 2h / 3.

What is the connection between the inscribed and circumscribed circles of an equilateral triangle?

The radius of the inscribed circle is one-third of the height of the triangle, while the radius of the circumscribed circle is two-thirds of the height. The ratio of the circumradius to the inradius is 2:1.

How can you determine the height of an equilateral triangle if the area is given?

If the area (A) is known, you can first calculate the side length (l) using the formula A = (l² * √3) / 4. Once the side length is known, use the formula for the height h = (l * √3) / 2.

What is the significance of the '2 3 4' sequence mentioned in the script?

The '2 3 4' sequence is a mnemonic to help remember the formula for the area of an equilateral triangle: A = (l² * √3) / 4. The sequence stands for the powers of 2, 3, and 4 in the formula components.

In the second exercise, how was the side length of the equilateral triangle determined?

In the second exercise, the area was given as 253√3. Using the area formula A = (l² * √3) / 4, the side length was calculated by isolating 'l' and solving for it. The result was l = 10 cm.

How is the formula for the area of an equilateral triangle applied in the third exercise?

In the third exercise, the side length was first determined from the relationship between the terms of the geometric progression. Then, the area was calculated using the formula A = (l² * √3) / 4, where 'l' was substituted into the equation.