Predict Market Volatility with 74% Accuracy Using this Key Metric
Summary
TLDRThis video discusses the limitations of assuming normality in stock log returns, commonly used in financial models like Black-Scholes. By introducing Quantile-Quantile (Q-Q) plots, the speaker highlights how real market data deviates from the normal distribution, particularly during periods of high volatility. Key concepts such as volatility clustering and regime shifts are explored, emphasizing the importance for traders to recognize when markets transition between regimes. The video also suggests that while historical data can inform strategies, its predictive power weakens during volatile periods, making real-time market observation and adaptation essential for active trading.
Takeaways
- 😀 The assumption of stock returns following a normal distribution, often used in financial models like Black-Scholes, is flawed in real market data.
- 😀 Real stock returns exhibit characteristics like fat tails, skewness, and excess kurtosis, which deviate from the normal distribution.
- 😀 Quantile-quantile (Q-Q) plots are a powerful statistical tool to compare the distribution of real market returns with a normal distribution.
- 😀 If market returns match a normal distribution, Q-Q plots show a 45-degree line. Any deviation indicates a difference between the distributions.
- 😀 Volatility clustering occurs when large price movements tend to happen close together, challenging the assumption that returns are independent.
- 😀 During periods of extreme market volatility, distributions can deviate significantly from historical normal expectations.
- 😀 Market regimes (bull, bear, or high-volatility markets) have distinct statistical properties that propagate over a sustained period.
- 😀 Identifying regime shifts in real-time is critical for active traders, as historical data may lose predictive power during such transitions.
- 😀 Signs of regime shifts include increased market correlations, higher intraday volatility, and appreciation of defensive assets like gold and bonds.
- 😀 Computational tools, like clustering algorithms and Markov models, can help detect regime shifts more reliably than intuition alone.
- 😀 The real challenge in detecting regime changes is that they are often difficult to pinpoint in real-time, despite certain telltale signs emerging.
Q & A
What is the normality assumption in finance, and why is it important?
-The normality assumption in finance suggests that stock log returns are normally distributed. This assumption is crucial because it forms the basis for many statistical models, including the Black-Scholes model, which is widely used for options pricing. It helps traders and financial professionals make predictions about stock price movements and calculate risk.
Why do actual stock returns often deviate from the normal distribution?
-Actual stock returns often deviate from the normal distribution because real-world data tends to exhibit 'fat tails', where extreme movements (large price changes) occur more frequently than a normal distribution would predict. This can be seen in higher-than-expected occurrences of 2-3 sigma moves and skewness in the data.
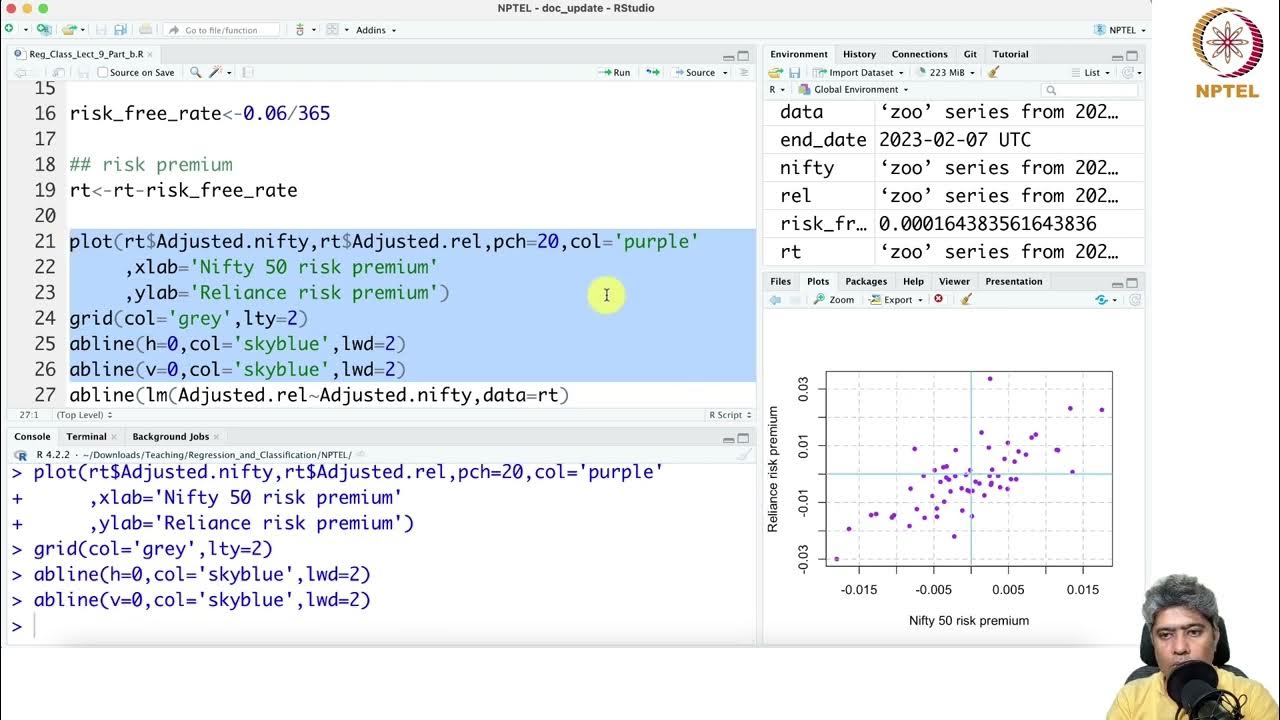
What are quantile-quantile plots (Q-Q plots), and how are they used in this context?
-Quantile-quantile (Q-Q) plots are a statistical tool used to compare two distributions by plotting their quantiles (i.e., their slices or segments) against each other. In this context, Q-Q plots are used to compare the distribution of stock returns with a normal distribution, helping to visually detect deviations from normality.
What does a straight 45-degree line in a Q-Q plot indicate?
-A straight 45-degree line in a Q-Q plot indicates that the two distributions being compared (e.g., stock returns and a normal distribution) are similar. If the plot closely matches this line, it suggests that the stock returns follow a normal distribution during the observed period.
What happens to the Q-Q plot during periods of extreme market volatility?
-During periods of extreme market volatility, the Q-Q plot deviates from the 45-degree line. This indicates that stock returns no longer align with the normal distribution, showing larger-than-expected movements, and highlighting phenomena like fat tails and skewness.
What is volatility clustering, and how is it observed in real market data?
-Volatility clustering refers to the tendency for large market moves (both up and down) to occur in clusters, i.e., when one large move happens, another is more likely to follow in the near future. This is evident in the Q-Q plot, where extreme moves are observed in close proximity, deviating from the normal distribution.
How do volatility clusters affect the probability of future market movements?
-Volatility clusters suggest that after a large move in the market (e.g., a 2-sigma move), the probability of another large move occurring within a short time frame (e.g., 10 days) increases significantly, from about 5% to 74%. This indicates that market behavior is not as random as assumed by the normal distribution.
What are market regimes, and why are they important for active traders?
-Market regimes refer to distinct phases in the market, such as bull markets, bear markets, or periods of high volatility, each characterized by unique statistical properties. Recognizing when the market transitions between these regimes is essential for active traders because it helps them adjust their strategies to the new market conditions.
Why does historical data become less reliable during regime shifts?
-Historical data becomes less reliable during regime shifts because the statistical properties of the market change. For example, a normal distribution might have accurately described stock returns in a stable market, but during high volatility, the market may exhibit skewness, fat tails, and other deviations that make previous models less effective.
What computational methods can help detect regime shifts in the market?
-Computational methods like clustering algorithms and Markov models, such as Gaussian Mixture Models (GMM), can help detect regime shifts. These models can analyze market data to identify changes in the underlying statistical properties, allowing traders to recognize when a market has transitioned into a new regime.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)