How to find Centroid of i section | Centre of gravity of I section | Problem 2 | Mechanics | 9.3
Summary
TLDRThis transcript seems to cover a technical discussion involving the analysis of composite areas, geometry, and mathematical calculations. It addresses the task of determining the center of a symmetrical composite figure, involving multiple steps such as dividing the figure into simpler shapes like rectangles and calculating areas and distances. The discussion includes various equations and references to real-world data (like meters, distances, and other measurements), possibly related to physical or engineering problems. The goal appears to be calculating and understanding the properties of a composite figure and finding its center of mass or area centroid.
Takeaways
- 😀 The script discusses the concept of symmetrical composite areas, with a focus on the application of these areas in geometric problems.
- 😀 A key problem involves calculating the centroid of a composite area, which consists of three symmetrical sections (rectangles).
- 😀 The problem includes determining the coordinates for the center of mass of a given figure using specific axes and measurements in meters.
- 😀 It emphasizes breaking down a composite area into simpler geometric shapes like rectangles and cylinders to facilitate calculations.
- 😀 The script mentions calculating the area of a complex figure by dividing it into three regular components for easier analysis.
- 😀 There's a reference to using certain tools or methods to simplify the process of finding the centroid of irregular shapes.
- 😀 Measurements such as area size, length, and height are discussed as essential components in calculating the centroid accurately.
- 😀 The concept of symmetry around a vertical axis is key to solving these geometric problems, and is crucial for dividing areas into equal parts.
- 😀 The role of scaling the calculations to proper units (e.g., meters and square meters) is underscored in the script for consistency and clarity.
- 😀 References to other unrelated topics, such as brands, technologies, and locations, appear sporadically, which may distract from the primary focus on geometry.
Q & A
What is the main focus of the script?
-The main focus of the script is on the calculation of areas and distances for a symmetric composite figure, involving concepts like axes, coordinates, and symmetry.
What is meant by 'composite area' in the script?
-A composite area refers to a figure that is made up of multiple simpler shapes (rectangles, cylinders, etc.) combined together to form a larger shape, which is symmetric about a vertical axis.
How is symmetry used in solving the problem?
-Symmetry is used to divide the composite area into equal parts, which simplifies the calculation of the center and total area. The figure is divided into three symmetrical sections along a vertical axis.
What is the significance of finding the 'center of the composite figure'?
-Finding the center of the composite figure is crucial for accurately calculating the total area and the distances of various parts of the figure from the central point. It helps in determining the coordinates with respect to the axes.
What steps are involved in solving the problem?
-The steps include dividing the composite figure into simpler sections, calculating the area and centroid for each part, and then using symmetry to find the total area and the center of the figure.
What is the role of the vertical axis in the problem?
-The vertical axis serves as the line of symmetry, dividing the figure into two equal parts. It plays a key role in determining the coordinates of the center and calculating the area of the figure.
How do the dimensions of the figure influence the calculations?
-The dimensions of the figure, such as height, length, and width, directly influence the area of each individual shape in the composite figure. These dimensions must be accurately measured to calculate the total area.
Why is there a mention of 'meters' in the script?
-The mention of 'meters' refers to the units of measurement for the distances and areas in the problem. These measurements are essential for accurately solving the geometry-related calculations.
What is the relationship between the 'composite figure' and 'rectangles' or 'cylinders' in the script?
-The composite figure is described as being made up of simpler shapes like rectangles and cylinders, which are easier to work with when calculating areas and centroids before combining them to solve for the total area.
What does the term 'axis' refer to in this script?
-In this context, 'axis' refers to the line used to divide the figure into symmetrical parts. It is used as a reference for measuring distances and calculating the center of the figure.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Grade 10 - Sector and Segment of a Circle (Arc Length) - Tagalog/English

Markov Chain Problem-I

MATHEMATICS PRACTICE QUESTIONS FOR THE 2025 TARUNA KEMALA BHAYANGKARA HIGH SCHOOL EXAM - PART 2

Relation Between Modulus of Elasticity and Modulus of Rigidity

Uncover the Math and Science in HIDDEN FIGURES (2016)
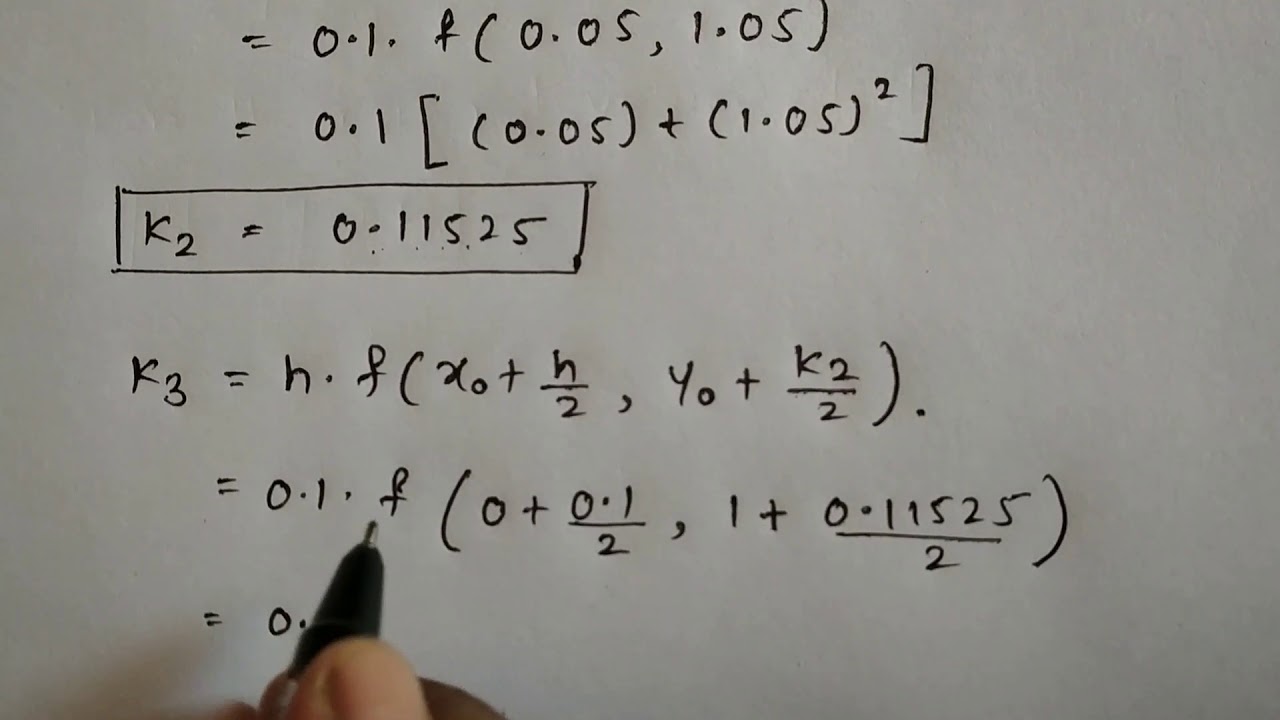
Numerical Solution of ODE by Runge - Kutta method of fourth order.
5.0 / 5 (0 votes)