🔵LA ELIPSE GEOMETRÍA ANALÍTICA [TRUCOS que necesitas saber ECUACIÓN GENERAL]🔵
Summary
TLDRIn this educational video, the professor explains the concept of an ellipse, starting with a simple definition involving two fixed points, known as foci, and the set of points where the sum of distances to the foci remains constant. Using a hands-on method with a string and nails to demonstrate the construction of an ellipse, the video also covers key mathematical principles such as the axes, the relationship between the major and minor axes, and the equation for horizontal and vertical ellipses. The explanation is enhanced with a detailed example, helping students understand the geometry and properties of ellipses.
Takeaways
- 😀 An ellipse is the set of points where the sum of distances to two fixed points, called foci, is constant.
- 😀 A hands-on method to construct an ellipse involves using two nails, a string, and a pencil to form the curve.
- 😀 The foci are key to defining an ellipse, and their location helps determine the shape and properties of the ellipse.
- 😀 In a horizontal ellipse, the equation takes the form: x²/a² + y²/b² = 1, where 'a' is the length of the major axis and 'b' is the minor axis.
- 😀 For a vertical ellipse, the equation is: x²/b² + y²/a² = 1, with the major axis now aligned with the y-axis.
- 😀 The center of the ellipse is the midpoint between the foci, and this point is used to establish the coordinates of other key points.
- 😀 The major axis (longer axis) is denoted by 'a' and the minor axis (shorter axis) by 'b'. In an ellipse, 'a' is always greater than 'b'.
- 😀 The focal distance 'c' can be found using the relationship: c² = a² - b², with 'c' representing the distance from the center to each focus.
- 😀 The concept of a 'semi-major axis' refers to half the length of the major axis, and similarly for the semi-minor axis.
- 😀 The focus of an ellipse can be located by adding or subtracting 'c' from the center point depending on the orientation of the ellipse (horizontal or vertical).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
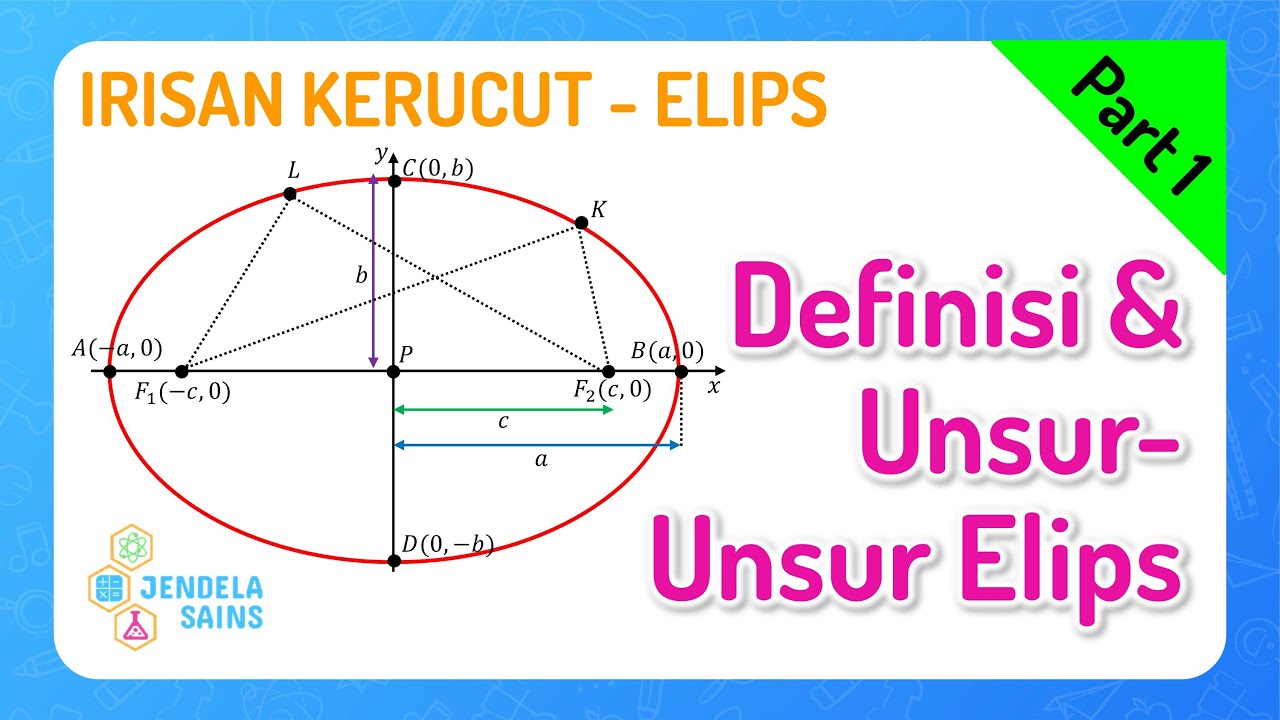
Irisan Kerucut - Elips • Part 1: Definisi, Unsur-Unsur, dan Jenis-Jenis Elips

Graphing Conic Sections Part 4: Hyperbolas

What is Ellipse? | Don't Memorise

Hyperbola (Part 1) | Conic Sections | Don't Memorise

How To Draw An Ellipse-Hommocks Earth Science Department

Gráfica y elementos de la Elipse conociendo la ecuación canónica | Ejemplo 2
5.0 / 5 (0 votes)