Como FATORAR PA=LDU e Resolver o Sistema de Equações Lineares - SEL13

Summary

Este video explica el proceso de descomposición LU, que consiste en factorizar una matriz en dos matrices triangulares: L (triangular inferior) y U (triangular superior). A través de una serie de operaciones elementales, como el escalonamiento de la matriz y el intercambio de filas, se obtienen los coeficientes necesarios para construir ambas matrices. Este método es útil para resolver sistemas de ecuaciones lineales y otras aplicaciones matemáticas. El video presenta ejemplos detallados de cómo aplicar estas técnicas paso a paso en matrices 3x3, proporcionando una comprensión clara del proceso de descomposición LU.

Takeaways

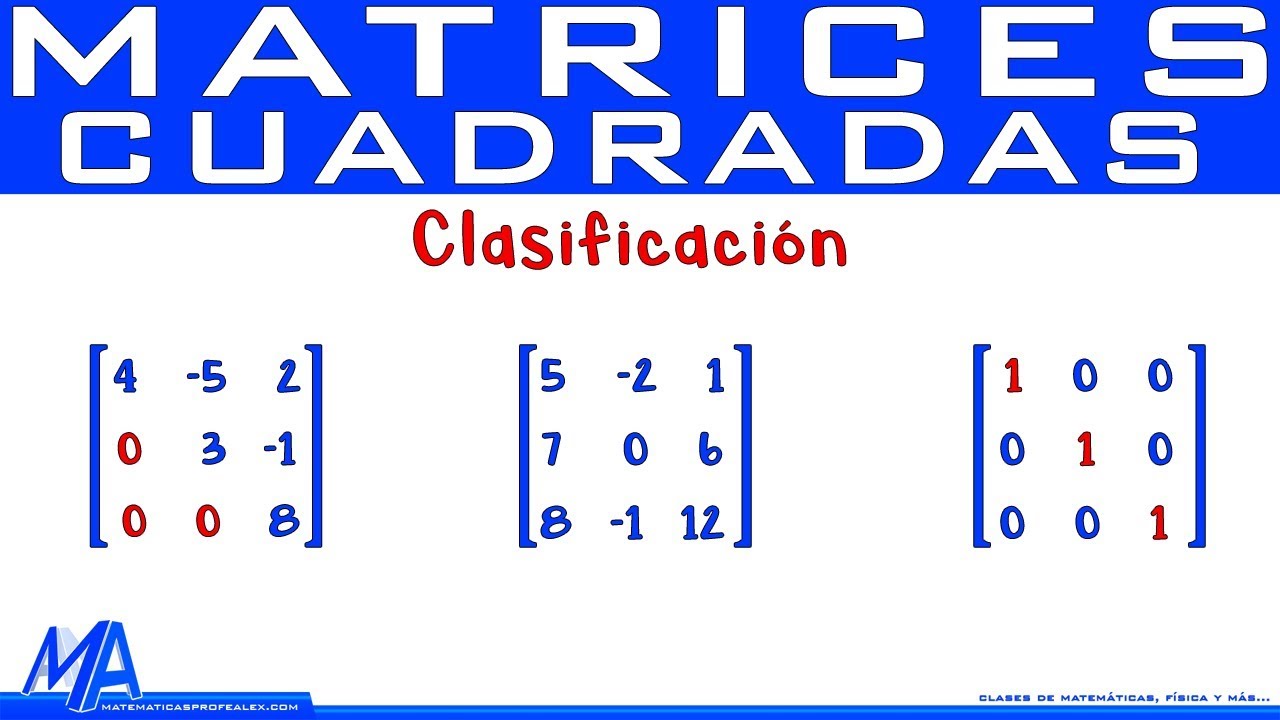
• 😀 La factorización LU es un proceso en el que una matriz se descompone en una matriz triangular inferior (L) y una matriz triangular superior (U).
• 😀 El proceso implica el uso de operaciones elementales, como la multiplicación de filas y la adición de múltiplos de una fila a otra, para transformar la matriz en una forma escalonada.
• 😀 Se utiliza la eliminación de Gauss para hacer ceros debajo del pivote en la matriz, lo cual es crucial para la factorización LU.
• 😀 La matriz L es triangular inferior y contiene los coeficientes de las operaciones elementales realizadas en el proceso de escalonamiento.
• 😀 La matriz U es triangular superior y contiene los resultados obtenidos después de aplicar las operaciones de eliminación.
• 😀 La factorización LU puede requerir la permutación de filas para asegurar la estabilidad numérica, especialmente cuando los pivotes son pequeños.
• 😀 El método implica la creación de una matriz de permutación (P), que almacena los cambios realizados en las filas de la matriz original.
• 😀 En algunos casos, la factorización LU se realiza con matrices más grandes, como una matriz de 3x3, para ilustrar el proceso de manera práctica.
• 😀 El procedimiento de factorización LU también está relacionado con la matriz diagonal, que se forma tomando los elementos de la diagonal principal de la matriz resultante.
• 😀 A través de este proceso, se obtiene una representación más sencilla de la matriz original, lo que facilita resolver sistemas de ecuaciones lineales y otros cálculos matriciales.

Q & A

¿Qué es la factorización LU de una matriz?

La factorización LU consiste en descomponer una matriz cuadrada en dos matrices: una triangular inferior (L) y una triangular superior (U). Esta técnica es útil para resolver sistemas de ecuaciones lineales y para otras operaciones algebraicas.

¿Qué operaciones elementales se utilizan en el proceso de factorización LU?

Las operaciones elementales son: intercambio de filas, multiplicación de una fila por un escalar y la adición de una fila a otra fila multiplicada por un escalar. Estas operaciones se usan para transformar la matriz en una forma escalonada.

¿Cuál es el propósito de la matriz de permutación?

La matriz de permutación se utiliza para registrar cualquier intercambio de filas que se realice durante el proceso de factorización LU, asegurando que el orden de las filas se mantenga correcto durante el escalonamiento.

¿Qué significa que una matriz sea triangular inferior?

Una matriz triangular inferior es aquella en la que todos los elementos por encima de la diagonal principal son cero. Solo los elementos de la diagonal y debajo de ella pueden ser distintos de cero.

¿Cómo se obtiene la matriz L en la factorización LU?

La matriz L se obtiene a partir de las operaciones de escalonamiento que transforman la matriz original en una matriz triangular inferior. Cada elemento debajo de la diagonal principal en L es el resultado de una operación elemental aplicada a las filas originales.

¿Cómo se transforma la matriz original en la forma escalonada?

La matriz original se transforma en forma escalonada mediante una serie de operaciones elementales, como la eliminación de elementos por debajo de la diagonal principal, utilizando los pivotes de cada columna para realizar las operaciones necesarias.

¿Qué papel juega la diagonal en la factorización LU?

La diagonal de la matriz U es crucial porque en la factorización LU, la matriz U tiene todos los elementos por encima de la diagonal no nulos, mientras que L tiene elementos solo en la diagonal y por debajo de ella. La diagonal en U contiene los factores que multiplican las filas de la matriz original.

¿Por qué se dividen las filas de la matriz en algunos puntos del proceso?

Las filas se dividen para asegurar que los elementos de la diagonal de la matriz U sean 1, facilitando la posterior resolución de sistemas de ecuaciones. Esta operación también estandariza los elementos de la matriz en su forma escalonada.

¿Qué sucede cuando se realiza un intercambio de filas en la factorización LU?

Cuando se realiza un intercambio de filas, la matriz de permutación se actualiza para reflejar este cambio. El intercambio de filas asegura que el pivote no sea cero y facilita la continuación del proceso de escalonamiento.

¿Qué significa el término 'escalonamiento' en el contexto de la factorización LU?

El escalonamiento se refiere al proceso de transformar una matriz en una forma triangular, donde los elementos debajo de la diagonal principal se vuelven cero mediante las operaciones elementales. Esto simplifica el sistema de ecuaciones representado por la matriz.