Learn FOIL In 7 Min (Fast Review On How To Multiply Binomials)
Summary
TLDRIn this video, a math teacher explains how to use the FOIL method to multiply binomials, a crucial algebraic skill. The teacher breaks down the FOIL acronym, covering the steps of First, Outer, Inner, and Last to help students understand the multiplication of two binomials. The video also emphasizes the importance of sign management and combining like terms. The teacher provides both a basic example and a more complex one involving negative terms, encouraging viewers to practice the technique to master the concept. This is an essential lesson for students in algebra courses and beyond.
Takeaways
- 😀 FOIL is a method used to multiply binomials, which are polynomials with two terms.
- 😀 The acronym FOIL stands for First, Outer, Inner, and Last—these steps guide you through the multiplication process.
- 😀 Binomials are polynomials with two terms, and the FOIL method only applies to multiplying two binomials.
- 😀 The FOIL method is essential in algebra and helps simplify the multiplication of binomials.
- 😀 The 'First' step involves multiplying the first terms of each binomial.
- 😀 The 'Outer' step involves multiplying the outer terms of the two binomials.
- 😀 The 'Inner' step involves multiplying the inner terms of the binomials.
- 😀 The 'Last' step involves multiplying the last terms of each binomial.
- 😀 After performing the FOIL steps, combine like terms to simplify the expression.
- 😀 Common mistakes occur when students overlook signs, especially with negative numbers. Always remember to include signs when multiplying.
- 😀 Practice is key to mastering the FOIL method, and repeated application helps solidify understanding.
Q & A
What is the FOIL method used for?
-The FOIL method is used to multiply two binomials in algebra. It is a specific procedure that stands for First, Outer, Inner, and Last, which helps organize the multiplication of terms from each binomial.
What does each letter in the FOIL acronym stand for?
-In the FOIL acronym, F stands for First, O stands for Outer, I stands for Inner, and L stands for Last. These refer to the order in which you multiply the terms from each binomial.
What is a binomial?
-A binomial is a polynomial that consists of exactly two terms, connected by either addition or subtraction. Examples include (x + y) or (2x - 3).
When should you use the FOIL method?
-You should use the FOIL method when multiplying two binomials, which are polynomials with two terms each. It is not used for monomials (single terms) or trinomials (three terms).
What are polynomials, and how are they related to the FOIL method?
-Polynomials are expressions with multiple terms, such as binomials and trinomials. The FOIL method is a technique for multiplying binomials, a specific type of polynomial.
What is the difference between a binomial and a trinomial?
-A binomial is a polynomial with two terms, whereas a trinomial is a polynomial with three terms. The FOIL method applies only to binomials, not trinomials.
How do you apply the FOIL method to the binomials (2x + 3) and (x - 1)?
-To apply FOIL, multiply: First: (2x * x) = 2x², Outer: (2x * -1) = -2x, Inner: (3 * x) = 3x, Last: (3 * -1) = -3. Then, combine the like terms: 2x² + (-2x + 3x) - 3, which simplifies to 2x² + x - 3.
Why is it important to keep track of positive and negative signs when using the FOIL method?
-It's important because the signs affect the multiplication result. For example, multiplying negative numbers results in positive products, while multiplying two positive numbers results in a positive product. Errors with signs can lead to incorrect solutions.
What happens if you incorrectly apply the FOIL method with a trinomial?
-If you incorrectly try to apply the FOIL method to a trinomial, you'll get an incorrect result. The FOIL method is specific to multiplying two binomials, and trinomial multiplication requires a different approach, often involving the distributive property.
How can you practice the FOIL method to improve your understanding?
-To improve your understanding, practice multiplying different binomials using the FOIL method. Work on both simple and more complex problems, ensuring you carefully follow the First, Outer, Inner, and Last steps and combine like terms.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Multiplication of Binomials using FOIL method and Vertical Form | Grade 8 | Q1 | Revised K-12 |

Foil Method Algebra, Binomials, Trinomials, Polynomials, Multiplication With Exponents

Difference of Two Squares Tagalog | Patterns and Algebra

Bentuk Aljabar (4) - Matematika Kelas 7
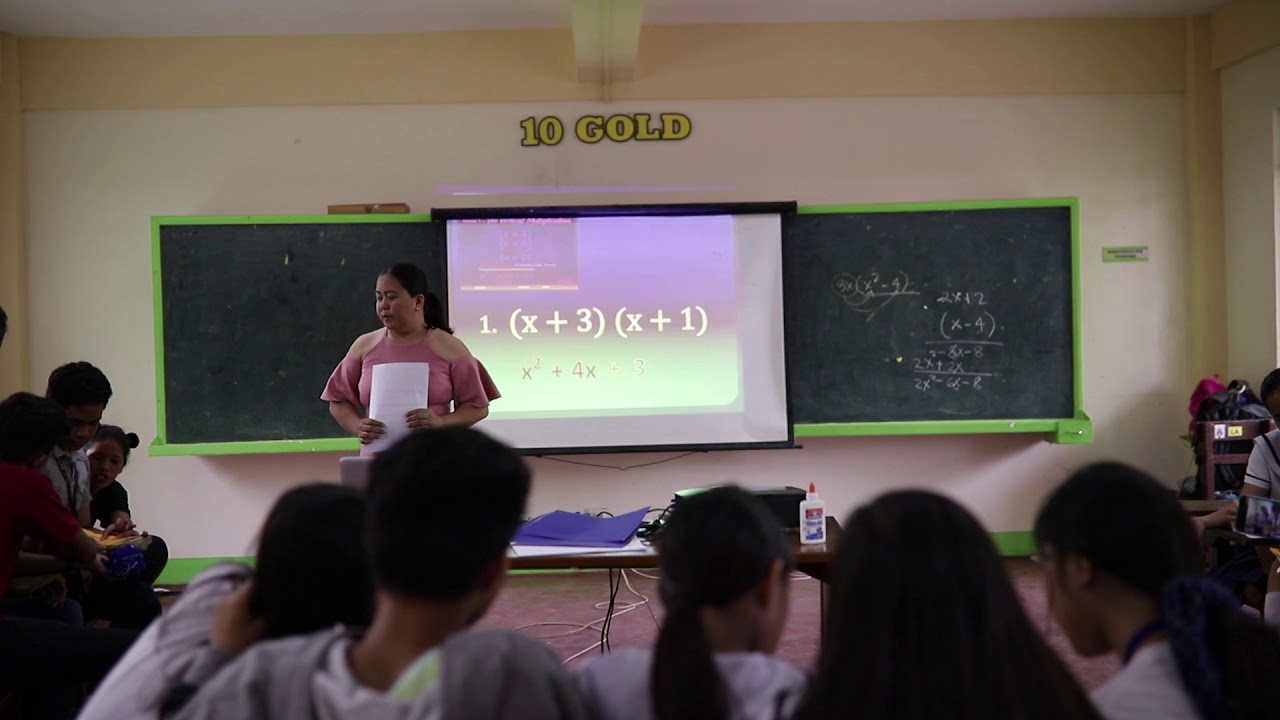
DepEd Teacher Class Demo - Math 7

NÚMEROS QUADRADOS PERFEITOS |COMO SABER SE UM NÚMERO É PERFEITO| Matemática - 6º ano \Prof. Gis/
5.0 / 5 (0 votes)