¿Es el 6174 el número más misterioso del mundo?
Summary
TLDREl número 6.174 es conocido como el más misterioso debido a su peculiaridad en un proceso matemático descubierto por el matemático indio D. R. Kaprekar en 1949. Este proceso consiste en formar el número más grande y el más pequeño posible con cuatro cifras, y restar uno al otro. Independientemente del número inicial, siempre se llega a 6.174, el cual se convierte en un punto fijo inalcanzable. Este fenómeno también se repite con otros números, como los llamados 'números kaprekar', que son puntos fijos para números de tres cifras (495) y se relacionan con un ciclo de cinco números para los de dos cifras. Además, se explora la posibilidad de constantes kaprekar para otros números de cifras, aunque no hay una única constante para todos. El video ofrece un desafío a los espectadores para practicar la resta y descubrir por sí mismos la magia detrás de este proceso matemático recreativo.
Takeaways
- 🔢 El número 6.174 es considerado uno de los más misteriosos debido a su propiedad sorprendente en un proceso matemático específico.
- 🧮 Selecciona un número de cuatro cifras, no todos iguales, y forma el número más grande y el más pequeño posible con esas cifras.
- ➖ Realiza la resta entre el número más grande y el número más pequeño, y a menudo se obtiene 6.174.
- 🔄 No importa el número inicial, la secuencia siempre converge a 6.174 si se sigue el proceso descrito.
- 🇮🇳 La constante de 6.174 fue descubierta por el matemático indio D. R. Kaprekar en 1949.
- 🎲 El proceso de Kaprekar no solo se aplica a números de cuatro cifras, sino que también tiene implicaciones para otros números de cifras.
- 📉 Para números de tres cifras, el análogo a 6.174 es 495, y es un punto fijo del proceso para números de tres cifras.
- 🔄 En el caso de dos cifras, no hay una única constante, sino un ciclo de cinco números (0, 1, 9, 8, 6) al que siempre se llega.
- 🔢 No existe una única constante o punto fijo para números de cifras superiores a cuatro, sino ciclos y puntos fijos que varían.
- 🤔 El número 6.174 y otros similares son ejemplos de matemáticas recreativas y pueden ser utilizados como ejercicios lúdicos para practicar la resta.
- 📚 Los números de Kaprekar son un tema interesante para explorar en clase y pueden ser utilizados para fomentar el aprendizaje de conceptos matemáticos.
- 🌐 El número 6.174 y el proceso de Kaprekar son un ejemplo de cómo la curiosidad y el juego con números pueden llevar a descubrimientos matemáticos.
Q & A
¿Por qué se considera al número 6.174 como uno de los más misteriosos?
-El número 6.174 es considerado misterioso debido a una propiedad sorprendente que aún no se sabe si obedece a alguna razón profunda. Este número siempre aparece como resultado de un proceso específico de formación de números con sus dígitos y realizando una resta.
¿Cuál es el proceso que se utiliza para llegar al número 6.174?
-El proceso consiste en elegir un número de cuatro cifras, formar el número más grande y el más pequeño posible con esos dígitos, y restar el segundo al primero. Repetir este proceso siempre lleva a 6.174.
¿Quién descubrió este proceso y por qué es significativo?
-El proceso fue descubierto por el matemático indio D. R. Kaprekar en 1949. Es significativo porque demuestra que 6.174 es un punto fijo del proceso para cualquier número de cuatro cifras que no tenga todos sus dígitos iguales.
¿Cómo se llama a este número en honor a su descubridor?
-En honor a D. R. Kaprekar, el número 6.174 es conocido como la constante de Kaprekar.
¿Qué sucede si se realiza el mismo proceso con el número 6.174 en sí mismo?
-Si se realiza el proceso con el número 6.174, el resultado también es 6.174, lo que demuestra que es un punto fijo del proceso y se mantiene allí invariablemente.
¿Existen constantes similares para números de diferente cantidad de dígitos?
-Sí, para números de tres dígitos, el número 495 tiene un comportamiento similar y es un punto fijo del proceso. Para dos dígitos, no hay un número único al que caiga todo, sino un ciclo de cinco números.
¿Cuál es el número de pasos máximos que se necesitan para llegar a 6.174 desde cualquier número de cuatro cifras?
-El número máximo de pasos necesarios para llegar a 6.174 desde cualquier número de cuatro cifras es ocho.
¿Cómo se podría utilizar este proceso en un entorno educativo?
-Este proceso puede utilizarse en un entorno educativo para practicar la resta de números. Los estudiantes podrían elegir un número de cuatro cifras y competir para ver quién llega primero a 6.174 y en cuántos pasos lo hace.
¿Por qué podría ser interesante para los estudiantes trabajar con este problema?
-Es interesante porque no solo practica la resta, sino que también introduce un elemento de juego y desafío, animando a los estudiantes a pensar críticamente y a resolver el problema de manera eficiente.
¿Qué es un número de la forma 16 un montón de 311, 17 otro montón de 6?
-Este tipo de número es un ejemplo de un número que sigue el patrón de la constante de Kaprekar, donde un montón de 3 y un montón de 4 resultan en el mismo número, es decir, 6.
¿Por qué podría ser útil la alfombra de Kaprekar para los estudiantes?
-La alfombra de Kaprekar, que muestra el número de pasos necesarios para llegar a 6.174 desde cada número de 0 al 9, puede ser útil para visualizar el proceso y comprender mejor cómo converge hacia el número 6.174.
¿Qué es un número hard sad en sánscrito?
-Un número hard sad en sánscrito significa 'grande alegría'. En el contexto del video, se refiere a los números que, al aplicar el proceso de Kaprekar, resultan en 6.174.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

🔶¿Qué es el VALOR ABSOLUTO de un número? ¿Qué son los NÚMEROS OPUESTOS?

NUMEROS PRIMOS Super facil

CONFIGURACIÓN ELECTRÓNICA ⚛️ Ejercicios resueltos

¿Por qué medimos el RITMO así? Compás de 4/4, 2/4, 6/8, 3/4... | Jaime Altozano
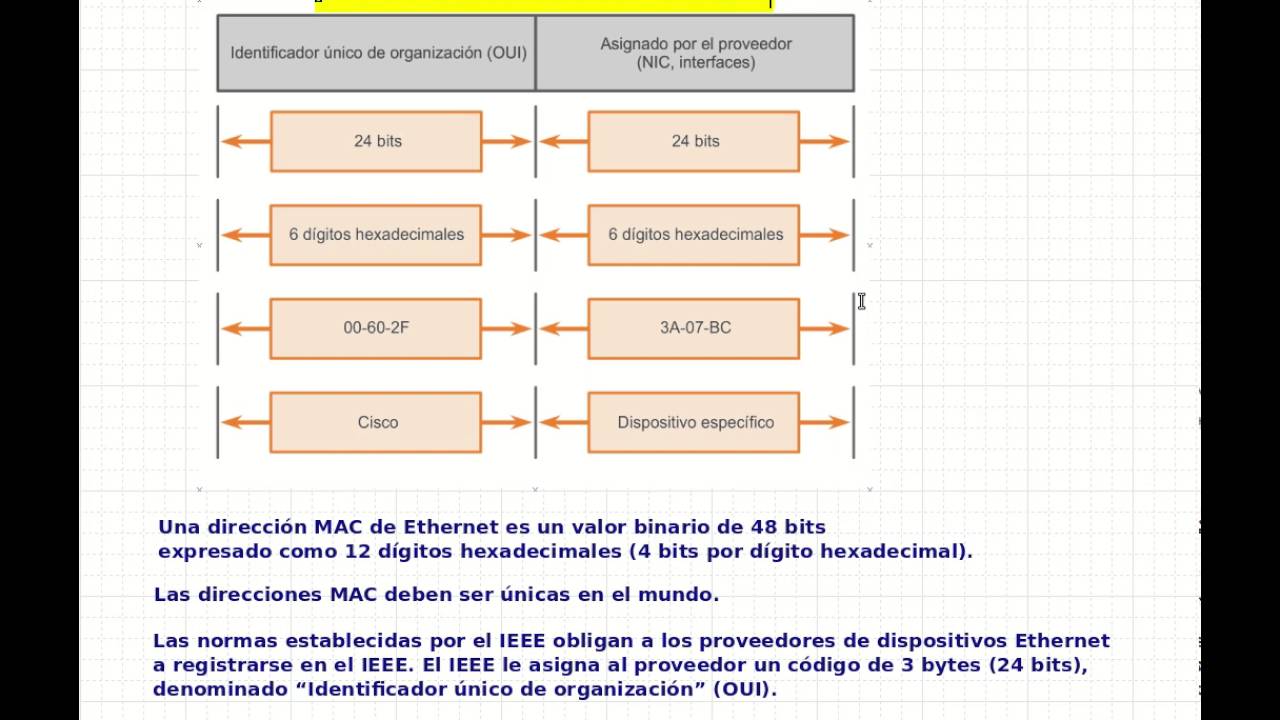
Que es la direccion MAC

TAMAÑOS de las BARRAS de acero corrugado EN PULGADAS, MILIMETROS Y NUMERO. ¿Cuáles DEBES utilizar?🤔

Matemáticas 22 ICFES 2014
5.0 / 5 (0 votes)
