Décrire un mouvement - BAC Terminale Spécialité Physique Chimie
Summary
TLDRDans cette vidéo, on explore comment décrire un mouvement avec précision en mécanique, en abordant les concepts fondamentaux de vecteurs position, vitesse et accélération. La vidéo détaille les dérivées de ces vecteurs pour comprendre les variations de position et de vitesse au cours du temps, et comment elles influencent l'accélération. On y traite des mouvements rectilignes uniformes, accélérés, et circulaires, tout en expliquant l'importance du repère de Freinet pour les mouvements circulaires. Des exercices pratiques illustrent ces notions pour permettre une meilleure compréhension des principes mécaniques.
Takeaways
- 😀 La position d'un objet dans l'espace se décrit par un vecteur OM, dont les coordonnées dépendent du temps et varient en fonction du mouvement de l'objet.
- 😀 Le vecteur vitesse est la dérivée du vecteur position par rapport au temps. Il représente la variation de la position sur un intervalle de temps très court.
- 😀 La vitesse peut être décomposée en trois composantes : vx, vy et vz, qui correspondent respectivement aux dérivées des coordonnées X, Y et Z par rapport au temps.
- 😀 Si un objet est immobile, ses coordonnées sont constantes et sa vitesse est donc nulle. Cela s'explique par la dérivée d'une constante égale à zéro.
- 😀 La dérivée d'une fonction affine (comme x(t) = at) est simplement la constante a, ce qui signifie que la vitesse dans ce cas est constante.
- 😀 La dérivée d'une fonction quadratique (comme x(t) = at²) est 2at, ce qui donne une vitesse qui augmente linéairement avec le temps.
- 😀 L'accélération est la dérivée de la vitesse par rapport au temps et représente la variation de la vitesse sur un intervalle très court.
- 😀 Dans un repère de Freinet utilisé pour les mouvements circulaires, la vitesse est tangentielle à la trajectoire, tandis que l'accélération a deux composantes : tangentielle et normale.
- 😀 Dans un mouvement circulaire uniforme, la vitesse reste constante, mais l'accélération est dirigée vers le centre du cercle (accélération centripète).
- 😀 Dans un mouvement rectiligne uniforme, la vitesse est constante et l'accélération est nulle, tandis que dans un mouvement uniformément accéléré, la vitesse change de manière régulière et l'accélération est constante.
- 😀 Les dérivées sont des outils mathématiques essentiels pour décrire les variations de position, de vitesse et d'accélération dans le cadre des exercices de mécanique.
Q & A
Comment définit-on le vecteur position dans un repère tridimensionnel ?
-Le vecteur position est défini comme le vecteur qui relie le centre du repère au point M qui nous intéresse. Ses coordonnées sont X(t), Y(t) et Z(t), représentant la position du point en fonction du temps.
Comment calcule-t-on le vecteur vitesse à partir du vecteur position ?
-Le vecteur vitesse est la dérivée du vecteur position par rapport au temps, c'est-à-dire la variation de la position pendant un intervalle de temps très court. Matériellement, cela se traduit par les dérivées des coordonnées X, Y, et Z du vecteur position.
Quelle est la dérivée d’une constante ?
-La dérivée d’une constante est égale à 0, car une constante ne varie pas au cours du temps.
Comment calcule-t-on la dérivée d'une fonction affine de la forme X(t) = a * t ?
-La dérivée d'une fonction affine, comme X(t) = a * t, est simplement la constante a. Cela résulte du fait que la pente de la fonction est constante.
Que signifie une dérivée d’une fonction carrée de la forme X(t) = a * t² ?
-La dérivée d'une fonction carrée, X(t) = a * t², donne 2 * a * t. Cela découle de la règle de dérivation des puissances de t.
Qu’est-ce qu’un vecteur accélération et comment est-il calculé ?
-Le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps. Il représente la variation de la vitesse pendant un court intervalle de temps. Le calcul du vecteur accélération se fait en dérivant chaque composante du vecteur vitesse.
Que représente le repère de Freinet et comment est-il utilisé ?
-Le repère de Freinet est un repère particulier utilisé pour décrire les mouvements circulaires. Il tourne en même temps que le point M, et il inclut les vecteurs normaux et tangents à la trajectoire.
Quels sont les deux composants du vecteur accélération dans un mouvement circulaire uniforme ?
-Dans un mouvement circulaire uniforme, le vecteur accélération se divise en deux parties : une partie tangente (liée à la variation de la vitesse tangentielle) et une partie normale (liée à la vitesse au carré divisée par le rayon de la trajectoire).
Dans quel cas un mouvement est-il rectiligne uniforme et quel est l'état de l'accélération dans ce cas ?
-Un mouvement est rectiligne uniforme lorsque la vitesse est constante. Dans ce cas, le vecteur vitesse est constant, et l'accélération est nulle, car il n'y a pas de variation de la vitesse.
Comment décrire un mouvement circulaire uniforme en termes de vecteurs vitesse et accélération ?
-Dans un mouvement circulaire uniforme, le vecteur vitesse est tangent à la trajectoire et de norme constante. Le vecteur accélération est perpendiculaire au vecteur vitesse et pointe vers le centre du cercle. Sa norme est constante et dépend de la vitesse et du rayon de la trajectoire.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Description des mouvements plans - Terminale Bacc français
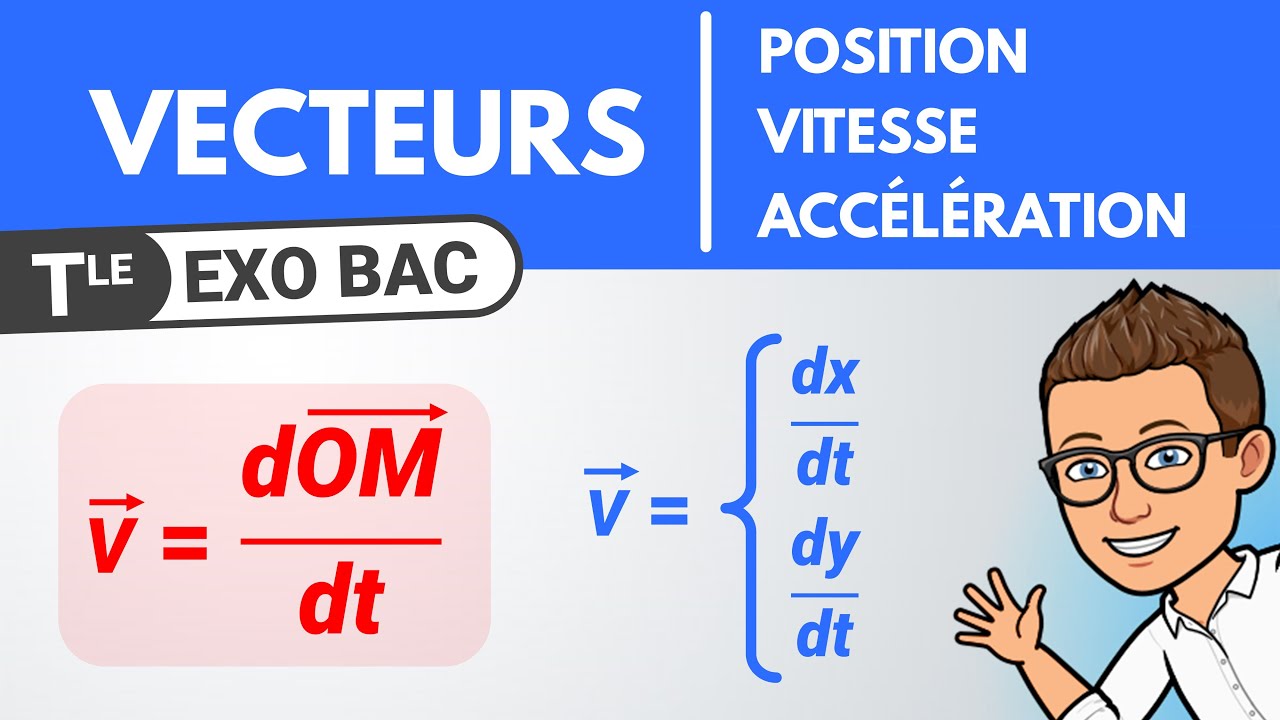
Vecteur position, vitesse et accélération pour décrire un mouvement | Terminale spécialité

Mouvement des satellites et des planètes - physique chimie terminale
Regressi 4 Le pointage vidéo
Modèles ondulatoire et particulaire de la lumière - cours de première spé de physique chimie

Mouvement dans un champ de pesanteur 🎯 Exercice BAC | Physique Terminale spécialité
5.0 / 5 (0 votes)
