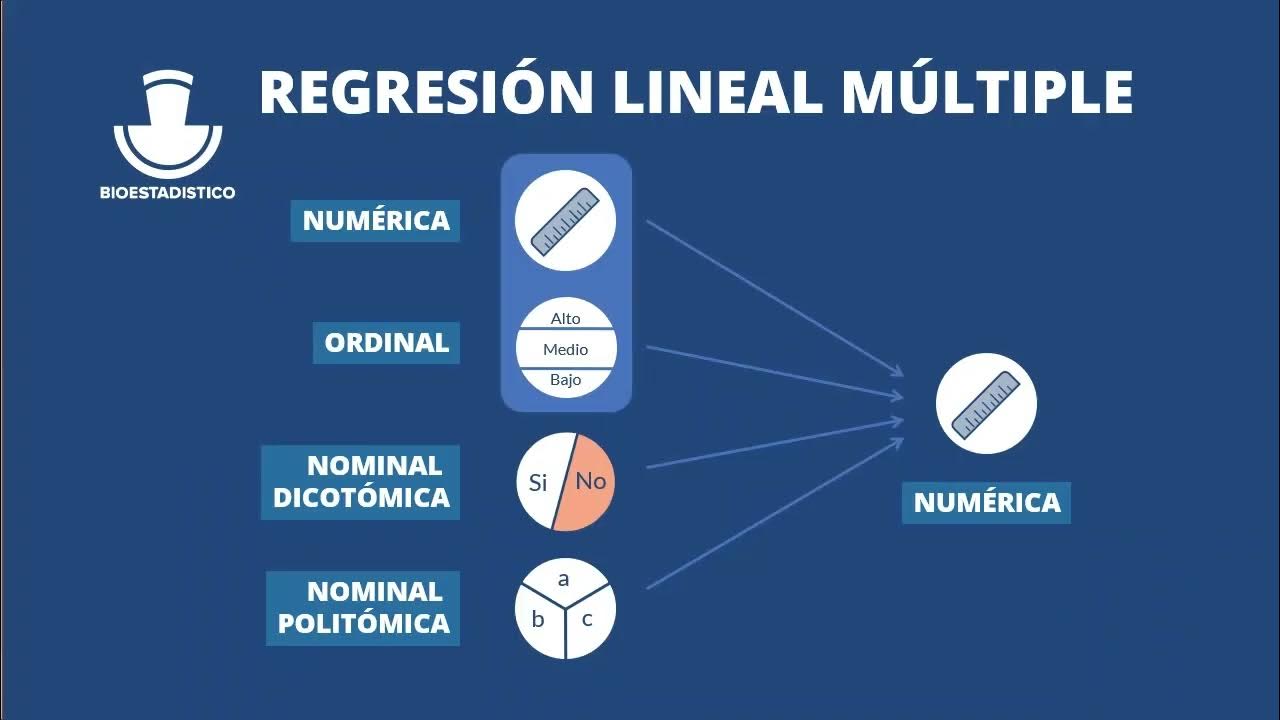
Regresión lineal múltiple - SPSS

Summary

En este análisis se aplica un modelo de regresión lineal múltiple para predecir el rendimiento académico en la universidad en función de la puntuación en selectividad y habilidades de búsqueda, evaluación, procesamiento y comunicación. Se destacan relaciones significativas entre las variables, como el impacto positivo de la selectividad y el efecto negativo del sexo masculino en el rendimiento. Se excluyen variables no significativas como las habilidades de evaluación y procesamiento. El modelo muestra un buen ajuste, con un R cuadrado superior a 0.50, evidenciando su capacidad para explicar el rendimiento académico.

Takeaways

• 😀 Se busca establecer un modelo de regresión múltiple en SPSS para predecir el rendimiento académico de los estudiantes.
• 📊 Se recogen datos sobre puntuaciones en selectividad, género y habilidades informacionales para el análisis.
• 📈 Es esencial comprobar la relación lineal entre las variables predictoras y la variable dependiente antes de aplicar el modelo.
• 🔍 Se utiliza la correlación de Pearson para evaluar la significancia y fuerza de las relaciones entre variables.
• 👩‍🎓 Las mujeres tienen una puntuación media más alta en la carrera, lo que se refleja en una correlación negativa con el género.
• 🔗 Las habilidades de búsqueda de información tienen una relación significativa y positiva con el rendimiento académico.
• ✂️ Se eliminan variables no significativas del modelo, como el procesamiento de información, para mejorar su precisión.
• ⚙️ El modelo final incluye las variables significativas: género, habilidades de búsqueda, y selectividad.
• 📉 El coeficiente de determinación (R²) es utilizado para evaluar la calidad del ajuste del modelo.
• 📝 El modelo permite predecir el rendimiento en la carrera basándose en el sexo y las habilidades informacionales del estudiante.

Q & A

¿Cuál es el objetivo principal del modelo de regresión presentado en el video?

El objetivo principal es predecir el rendimiento académico de un estudiante a partir de su puntuación en selectividad y sus habilidades en búsqueda, evaluación, procesamiento y comunicación de información, así como su género.

¿Qué variables se consideran como independientes en el modelo?

Las variables independientes incluyen la puntuación en selectividad, las habilidades de búsqueda, procesamiento y comunicación, y el género del estudiante.

¿Cómo se transforma la variable de género para el análisis?

La variable de género se convierte en numérica, asignando 0 a las mujeres y 1 a los hombres, para facilitar su inclusión en el modelo de regresión.

¿Qué método se utiliza para comprobar la relación lineal entre las variables?

Se utiliza el cálculo de coeficientes de correlación de Pearson para evaluar la relación lineal entre las variables predictoras y la variable dependiente.

¿Por qué se elimina la variable de evaluación en el análisis de regresión?

La variable de evaluación se elimina porque no muestra una relación significativa con el rendimiento en la carrera, lo que significa que no contribuye al modelo predictivo.

¿Qué indica un valor de R cuadrado superior a 0.50 en el modelo?

Un valor de R cuadrado superior a 0.50 indica que el modelo tiene un buen ajuste, explicando más del 50% de la variabilidad de la variable dependiente.

¿Qué se evalúa en la tabla de coeficientes del modelo?

En la tabla de coeficientes se evalúan los coeficientes no estandarizados y estandarizados, así como la significación de cada variable en relación con la variable dependiente.

¿Cuál es la ecuación final del modelo de regresión?

La ecuación del modelo de regresión es: Rendimiento = β0 + β1(Selectividad) + β2(Búsqueda) + β3(Género), donde β0 es la constante y β1, β2, y β3 son los coeficientes de las variables.

¿Qué significa una correlación negativa entre el género y la puntuación en la carrera?

Una correlación negativa indica que, en promedio, las mujeres tienden a obtener puntuaciones más altas en la carrera que los hombres, según el modelo.

¿Cómo afecta la puntuación en la búsqueda de información al rendimiento en la carrera?

El modelo indica que una mayor puntuación en la búsqueda de información se asocia con una disminución en el rendimiento en la carrera, con una reducción de aproximadamente 0.48 puntos por cada punto adicional en búsqueda.