Cómo cálcular la velocidad tangencial y la aceleración centripeta - MCU

Summary

In this educational video, the process of calculating the tangential velocity and centripetal acceleration of a satellite in uniform circular motion around Earth is explained. Using the given data, the presenter guides viewers through converting units, applying relevant equations, and performing the necessary calculations step by step. The exercise highlights the importance of visualizing the problem through diagrams and demonstrates how to work with scientific notation. The video ends with clear calculations, showing the satellite's tangential speed and centripetal acceleration, emphasizing key concepts and offering helpful tips for solving physics problems.

Takeaways

• 😀 The video introduces the topic of circular uniform motion, focusing on calculating tangential velocity and centripetal acceleration.
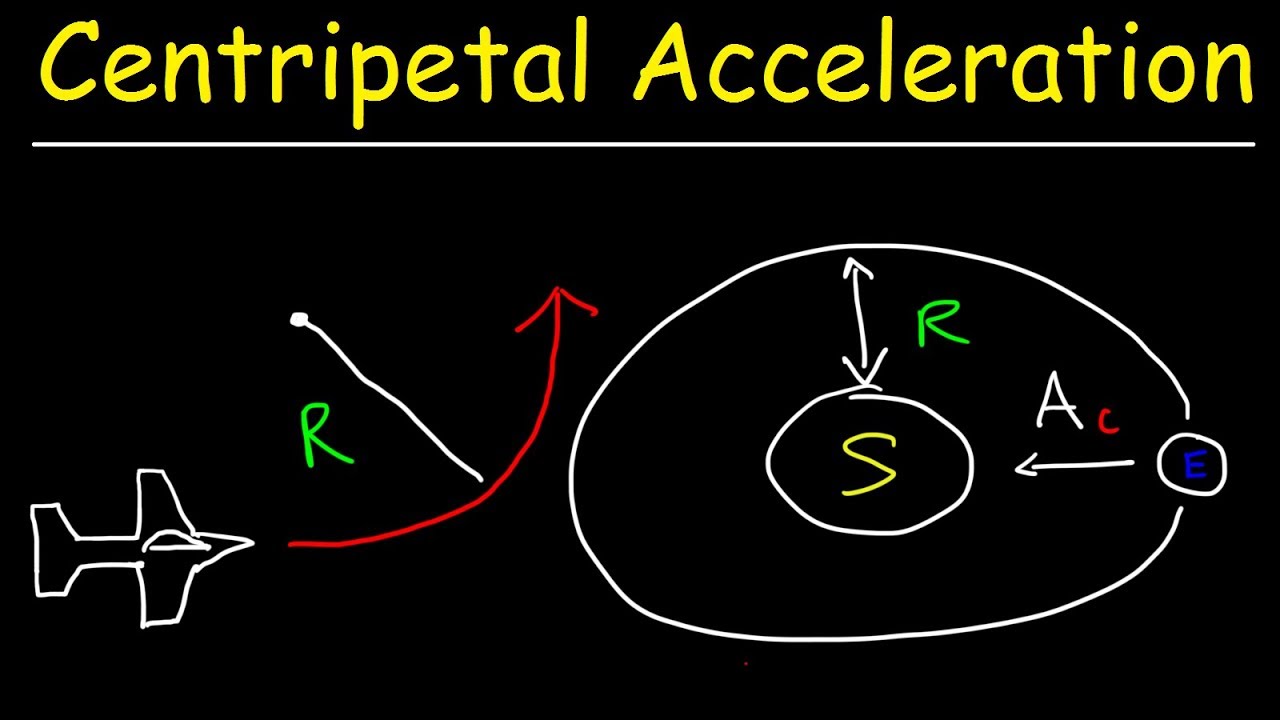
• 😀 The problem in the video involves a satellite orbiting Earth at an altitude of 500 km, and it asks to calculate the tangential velocity and centripetal acceleration.
• 😀 The radius of Earth is provided as 6.4 x 10^6 meters, which is essential in solving the problem.
• 😀 The satellite completes one revolution every 90 minutes, which is the period (T) of the satellite's orbit.
• 😀 The importance of drawing a schematic diagram of the problem is emphasized to visualize the motion and the relevant variables.
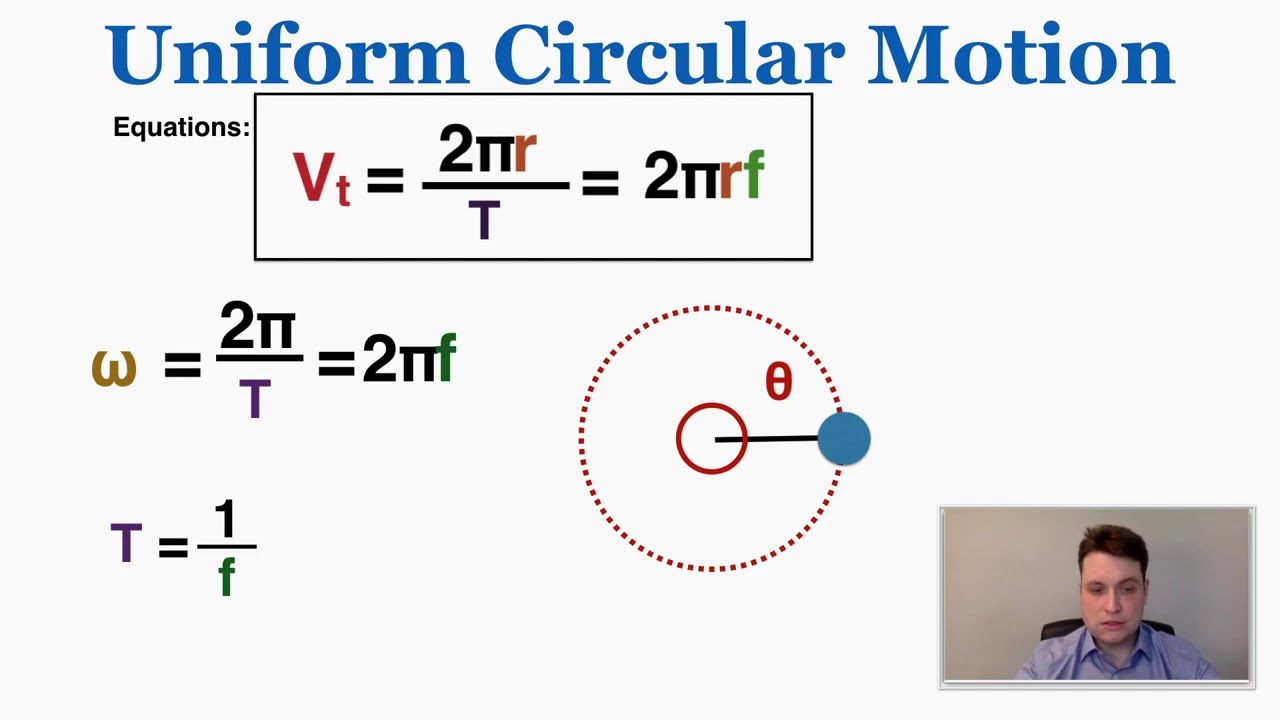
• 😀 To solve for tangential velocity, the formula used is: v = r * ω, where r is the radius of the orbit and ω is the angular velocity.
• 😀 The angular velocity (ω) is calculated as 2π divided by the period in seconds, resulting in ω = 1.16 x 10^-3 radians per second.
• 😀 The total radius of the satellite's orbit is the sum of Earth's radius and the satellite's altitude (r_total = 6.9 x 10^6 meters).
• 😀 The calculated tangential velocity is 8.0 x 10^3 m/s, which is a very high speed for the satellite.
• 😀 For centripetal acceleration, the formula a_c = v^2 / r is used, where v is the tangential velocity and r is the orbit's radius.
• 😀 The final centripetal acceleration of the satellite is calculated to be 9.3 m/s^2, which is directed towards the center of the Earth.
• 😀 The video encourages viewers to subscribe to the channel and provides tips for solving similar physics problems in future videos.

Q & A

What is the primary objective of the exercise in the video?

The primary objective of the exercise is to calculate the tangential velocity and centripetal acceleration of a satellite orbiting the Earth.

What is the given altitude of the satellite above the Earth's surface?

The satellite's altitude above the Earth's surface is given as 500 km or 5.0 x 10^5 meters.

What is the period of the satellite's orbit?

The satellite completes one revolution every 90 minutes. This is the period of its orbit.

How do you convert the period from minutes to seconds?

To convert the period from minutes to seconds, you multiply by 60. For 90 minutes, the period in seconds is 90 * 60 = 5400 seconds.

Why is it important to sketch a diagram when solving physics problems like this?

Sketching a diagram helps to visually understand the situation, which aids in identifying and organizing the necessary data and relationships for solving the problem.

What formula is used to calculate the tangential velocity of the satellite?

The formula to calculate the tangential velocity is: v_t = r * ω, where r is the radius of the orbit, and ω is the angular velocity.

How is the angular velocity (ω) related to the period of the satellite's orbit?

Angular velocity is calculated using the formula ω = 2π / T, where T is the period of the satellite's orbit.

What is the total radius of the satellite's orbit?

The total radius of the satellite's orbit is the sum of the Earth's radius (6.4 x 10^6 meters) and the satellite's altitude (5.0 x 10^5 meters), resulting in a total radius of 6.9 x 10^6 meters.

What is the calculated tangential velocity of the satellite?

The calculated tangential velocity of the satellite is 8.0 x 10^3 meters per second (or 8000 m/s).

How is the centripetal acceleration of the satellite calculated?

Centripetal acceleration is calculated using the formula: a_c = v_t^2 / r, where v_t is the tangential velocity and r is the radius of the orbit.