Funciones de varias variables. Definición, dominio y rango
Summary
TLDRIn this video, the instructor delves into functions of multiple variables, explaining their real-world applications like income calculation, production evaluation, and apparent temperature based on humidity and temperature. The lesson covers the concept of domain and range for functions of two variables, using the function f(x, y) = 3x^3 - 4y - 1 as an example. The instructor illustrates how to compute the domain (all of R²) and range (all real numbers) by evaluating specific points. The video offers a clear understanding of these concepts, providing both theoretical and practical insights.
Takeaways
- 😀 Functions of multiple variables are useful in real-life scenarios such as product sales, production, temperature, and humidity indexes.
- 😀 The domain of a function of multiple variables is a subset of RN, where n is greater than 1, and it represents the input space of the function.
- 😀 The range of a function is the set of output values, also known as the images of the function, denoted as 'range of F'.
- 😀 A function of multiple variables assigns a real number to each point in its domain, transforming inputs into outputs.
- 😀 The domain of a function can be visualized as a region in a plane, with each point in the region being mapped to a real number.
- 😀 A practical example of a function of multiple variables is the temperature-humidity index, where temperature and humidity are the variables influencing the result.
- 😀 The function F(x, y) = 3x^3 - 4y - 1 is an example of a function with two variables, x and y.
- 😀 To evaluate a function at a point, substitute the values of the variables into the function's equation and perform the necessary calculations.
- 😀 The function F(x, y) is continuous and well-defined for all real values of x and y, with no issues when substituting values.
- 😀 The domain of the function F is the entire 2D plane, represented as R^2, meaning all pairs of real numbers (x, y) are valid inputs for the function.
- 😀 The range of the function F is all real numbers (R), as it can produce any real number as an output depending on the values of x and y.
Q & A
What is the main focus of this video?
-The video focuses on introducing and explaining functions of several variables, specifically in the context of vector calculus using GeoGebra.
Why are functions of several variables important in real life?
-Functions of several variables are used to model real-world situations where multiple factors interact, such as calculating profit based on product sales or determining temperature-humidity indexes.
What is the domain of a function of several variables?
-The domain of a function of several variables is a subset of R^n (n-dimensional space), and it consists of all points where the function is defined.
How is the range of a function of several variables defined?
-The range of a function is the set of all possible output values (real numbers) the function can produce, based on the inputs within its domain.
Can you give an example of a real-world function of two variables?
-Yes, the body surface area, which depends on both a person's weight and height, is an example of a real-world function of two variables.
What does the function f(x, y) = 3x^3 - 4y - 1 represent?
-The function f(x, y) = 3x^3 - 4y - 1 is an example of a function of two variables where the output is a real number based on inputs x and y, representing a transformation of points from R^2 to real numbers.
How can the function f(x, y) = 3x^3 - 4y - 1 be evaluated at specific points?
-To evaluate the function at specific points, substitute the values of x and y into the equation and perform the calculations. For example, f(1,1) results in -2.
What happens when you substitute x = 0 into the function f(x, y) = 3x^3 - 4y - 1?
-When x = 0, the function simplifies to f(0, y) = -4y - 1, which is a linear function of y with a range of all real numbers.
What can be concluded about the domain and range of the function f(x, y) = 3x^3 - 4y - 1?
-The domain of the function is all points in R^2 (the entire two-dimensional plane), and the range is all real numbers, R, as the function can take any real value depending on the inputs.
Why is the range of the function f(x, y) = 3x^3 - 4y - 1 all real numbers?
-The range is all real numbers because, when evaluated for specific values of x and y, the function can yield any real number based on the combinations of x and y.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Logika Fuzzy MAMDANI dengan MATLAB | Fuzzy Logic Designer Toolbox

Geo X. 29. Pengukuran Unsur-unsur Cuaca dan Intepretasi Data Cuaca
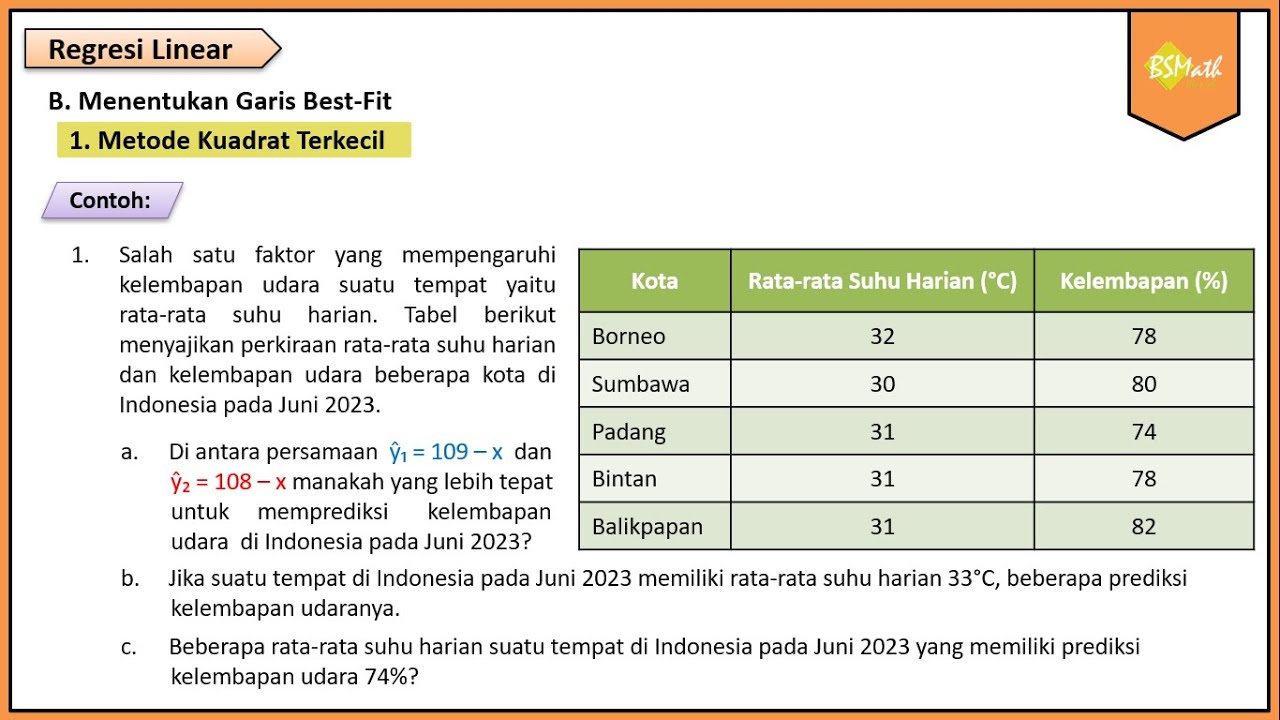
Contoh Soal dan Pembahasan Metode Kuadrat Terkecil - Matematika Wajib Kelas XI Kurikulum Merdeka

specific heat capacity explained

Estado dos Gases

Random Variables and Probability Mass/Density Functions
5.0 / 5 (0 votes)