Linear Expansion of Solids, Volume Contraction of Liquids, Thermal Physics Problems
Summary
TLDRThis educational video delves into the concept of thermal expansion, illustrating how objects change in size when subjected to temperature variations. It explains that solids expand with heat and contract with cold, with the change in length (ΔL) being proportional to the original length, temperature change, and a material-specific coefficient (α). The video uses practical examples, such as an aluminum bar and a lead plate, to demonstrate calculations for length and area changes due to temperature. It also covers volume expansion, introducing the coefficient of volume expansion (β) and its relation to linear expansion (α), with examples including brass and water. The video simplifies complex physics into accessible explanations, making it an informative resource for learners.
Takeaways
- 🔥 Thermal expansion is the process where objects increase in size when heated and decrease when cooled.
- 📏 The change in length (ΔL) of an object due to temperature change is directly proportional to its original length (L) and the temperature change (ΔT).
- 🌡️ The coefficient of linear expansion (α) is a material-dependent constant that relates the change in length to the temperature change.
- 📐 For a given material, the longer the object, the greater the change in length for the same temperature change.
- 🛠️ The formula for calculating the change in length is ΔL = α * L * ΔT, where units of length must be consistent.
- 📉 When the temperature decreases, ΔL is negative, indicating contraction of the object.
- 📏 The new length of an object can be found by adding the original length to the change in length (L_new = L + ΔL).
- 🔩 The area of an object expands or contracts when its length and width change due to temperature variations.
- 📐 The change in area (ΔA) can be approximated by ΔA ≈ 2 * L * W * α * ΔT for small temperature changes.
- 💧 Volume expansion occurs similarly to linear expansion, with the change in volume (ΔV) related to the original volume, the coefficient of volume expansion (β), and the temperature change.
- 📦 For solids, β is approximately three times α, simplifying the volume expansion calculation to ΔV = V * β * ΔT.
Q & A
What is thermal expansion?
-Thermal expansion is the phenomenon where objects increase in size when heated and decrease in size when cooled.
How does the temperature change affect the length of a solid bar?
-When the temperature of a solid bar is increased, it expands and gets longer; when the temperature is decreased, it contracts and gets shorter.
What is Delta L in the context of thermal expansion?
-Delta L represents the change in length of an object due to a change in temperature.
What is the relationship between the change in length (Delta L) and the original length (L) of an object?
-The change in length (Delta L) is proportional to the original length (L) of the object, meaning a longer object will experience a greater change in length for the same temperature change.
What is the coefficient of linear expansion (Alpha), and how does it relate to the material of an object?
-The coefficient of linear expansion (Alpha) is a constant that depends on the type of material and determines how much an object's length changes with temperature.
How can you calculate the change in length of an aluminum bar when its temperature is increased?
-You can calculate the change in length (Delta L) using the formula: Delta L = Alpha * L0 * Delta T, where Alpha is the coefficient of linear expansion, L0 is the original length, and Delta T is the change in temperature.
What is the new length of a bar after a temperature change, and how do you calculate it?
-The new length of a bar after a temperature change is the original length plus the change in length (L_new = L0 + Delta L).
How does thermal expansion affect the area of a solid plate?
-Thermal expansion affects the area of a solid plate by causing it to expand in all directions, increasing both its length and width, which results in an increased area.
What is the formula for calculating the change in area (Delta A) of a solid plate due to thermal expansion?
-The formula for calculating the change in area (Delta A) is: Delta A ≈ l0 * w0 * (2 * Alpha * Delta T), where l0 and w0 are the original length and width, Alpha is the coefficient of linear expansion, and Delta T is the change in temperature.
How does the volume of an object change with temperature, and what is the coefficient of volume expansion (Beta)?
-The volume of an object changes with temperature due to thermal expansion, and the coefficient of volume expansion (Beta) is used to calculate this change, typically being approximately three times the linear expansion coefficient (Alpha) for most solids.
What is the relationship between linear expansion and volume expansion in terms of their coefficients?
-For most solids, the coefficient of volume expansion (Beta) is approximately three times the coefficient of linear expansion (Alpha), reflecting the three-dimensional nature of volume change compared to the one-dimensional change in length.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Dilatação Térmica - Brasil Escola

Thermal Volume Expansion

Pemuaian Zat Padat, Zat Cair, dan Zat Gas (Pemuaian Panjang, Luas, dan Volume)
Suhu dan Kalor Fisika Kelas 11 - Part 2 : Pemuaian Zat Padat, Zat Cair, Zat Gas

Фізика 8. Урок - Тепловий стан. Температура та її вимірювання. Презентація для 8 класу
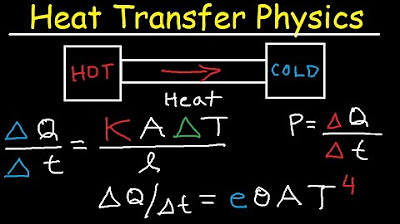
Thermal Conductivity, Stefan Boltzmann Law, Heat Transfer, Conduction, Convecton, Radiation, Physics
5.0 / 5 (0 votes)