Intervalo de confianza de la proporción poblacional
Summary
TLDREl guión proporciona una explicación detallada sobre cómo calcular el intervalo de confianza para una proporción de la población, utilizando muestras grandes. Se mencionan las condiciones necesarias para que la distribución muestral sea aproximadamente normal, incluyendo que n*p y n*(1-p) sean mayores o iguales a 5. Se utiliza la fórmula de la proporción más o menos z*(raíz cuadrada de p*(1-p)/n) para calcular el intervalo. Se ilustra con ejemplos, calculando intervalos de confianza al 90% y al 95% para una muestra de 800 unidades con una proporción de 0.70, utilizando la hoja de cálculo para encontrar el valor z y calcular el margen de error.
Takeaways
- 📊 La estimación de un intervalo de proporción de la población se realiza para muestras grandes (n ≥ 30) y asume que la distribución muestral de la proporción p es aproximadamente normal.
- 🔍 Para que esta aproximación sea válida, deben cumplirse dos condiciones: n*p ≥ 5 y n*(1-p) ≥ 5, donde n es el tamaño de la muestra y p es la proporción.
- 📉 La desviación estándar de la proporción muestral es dada por la raíz cuadrada de (p*(1-p))/n.
- 📚 El intervalo de confianza para una proporción se calcula con la fórmula: proporción muestral ± z*(raíz cuadrada de p*(1-p)/n), donde z es el valor zalfa/2 de la distribución normal estándar.
- 🎯 El valor zalfa/2 se determina por el nivel de confianza (1 - alfa) y representa la cantidad de área bajo la curva normal a la derecha del punto z.
- 📉 El margen de error es el producto del valor z y la desviación estándar de la proporción muestral.
- 📈 Se muestra un ejemplo práctico donde se calcula el intervalo de confianza al 90% para una muestra de 800 unidades con una proporción de 0.70.
- 🔢 En el ejemplo, se verifican las condiciones para la aproximación normal, y se calcula el valor z correspondiente al nivel de confianza deseado (1.64 para un 90% de confianza).
- 📝 Se describe el proceso de calcular el intervalo de confianza utilizando una hoja de cálculo, incluyendo el uso de la función de distribución normal inversa para encontrar el valor z.
- 🔄 Se ilustra cómo cambiar el nivel de confianza afecta el valor de z y, en consecuencia, el intervalo de confianza resultante, como se muestra en el ejemplo de un intervalo de confianza al 95%.
- 📋 Finalmente, se explica cómo interpretar los intervalos de confianza en términos de porcentaje, indicando la probabilidad de que la proporción de la población esté dentro de cierto rango.
Q & A
¿Cuándo es apropiado usar una distribución normal para estimar una proporción de la población?
-Es apropiado cuando el tamaño de la muestra es mayor o igual a 30 y se cumplen las condiciones de n * p ≥ 5 y n * (1 - p) ≥ 5, donde n es el tamaño de la muestra y p es la proporción.
¿Qué es la desviación estándar de una proporción muestral y cómo se calcula?
-La desviación estándar de una proporción muestral es igual a la raíz cuadrada de (p * (1 - p)) / n, donde p es la proporción en la muestra y n es el tamaño de la muestra.
¿Cómo se determina el valor z para un intervalo de confianza específico?
-El valor z se determina a partir de una tabla de valores z, buscando el valor que corresponde a la probabilidad complementaria a la mitad del nivel de confianza (alfa/2).
¿Cuál es la fórmula para calcular el intervalo de confianza de una proporción?
-La fórmula es p ± z * sqrt((p * (1 - p)) / n), donde p es la proporción muestral, z es el valor z correspondiente al nivel de confianza y n es el tamaño de la muestra.
¿Cómo se calcula el margen de error en el intervalo de confianza de una proporción?
-El margen de error se calcula como z * la desviación estándar de la proporción, donde z es el valor zeta correspondiente al nivel de confianza.
¿Qué tamaño de muestra (n) se utiliza en el ejemplo proporcionado en el guion?
-En el ejemplo, el tamaño de la muestra (n) es de 800 unidades.
¿Cuál es la proporción (p) en la muestra del ejemplo del guion?
-La proporción (p) en la muestra del ejemplo es de 0.70.
¿Cuál es el nivel de confianza utilizado en el primer ejemplo del guion y cuál es el intervalo de confianza resultante?
-El nivel de confianza utilizado en el primer ejemplo es del 90%, y el intervalo de confianza resultante es de 0.6734 a 0.7266.
¿Cómo se utiliza una hoja de cálculo para calcular el intervalo de confianza de una proporción?
-Se utiliza la función de distribución normal estándar inversa para encontrar el valor z, y luego se aplica la fórmula del intervalo de confianza en la celda correspondiente.
¿Cuál es el valor z para un nivel de confianza del 95% y cómo se determina?
-El valor z para un nivel de confianza del 95% es 1.96, determinado a través de una tabla de valores z buscando la probabilidad complementaria a 0.025 (alfa/2).
¿Cuál es el intervalo de confianza para un nivel del 95% en el segundo ejemplo del guion?
-El intervalo de confianza para un nivel del 95% es de 0.6682 a 0.7318.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Estimación por intervalo de una media poblacional: desviación estándar conocida

Estimación de la proporción poblacional

Estimación de parámetros - Parte 1

Intervalo de confianza para la proporción de la población

Tamaño de Muestra para Variables Cuantitativas con Población Finita
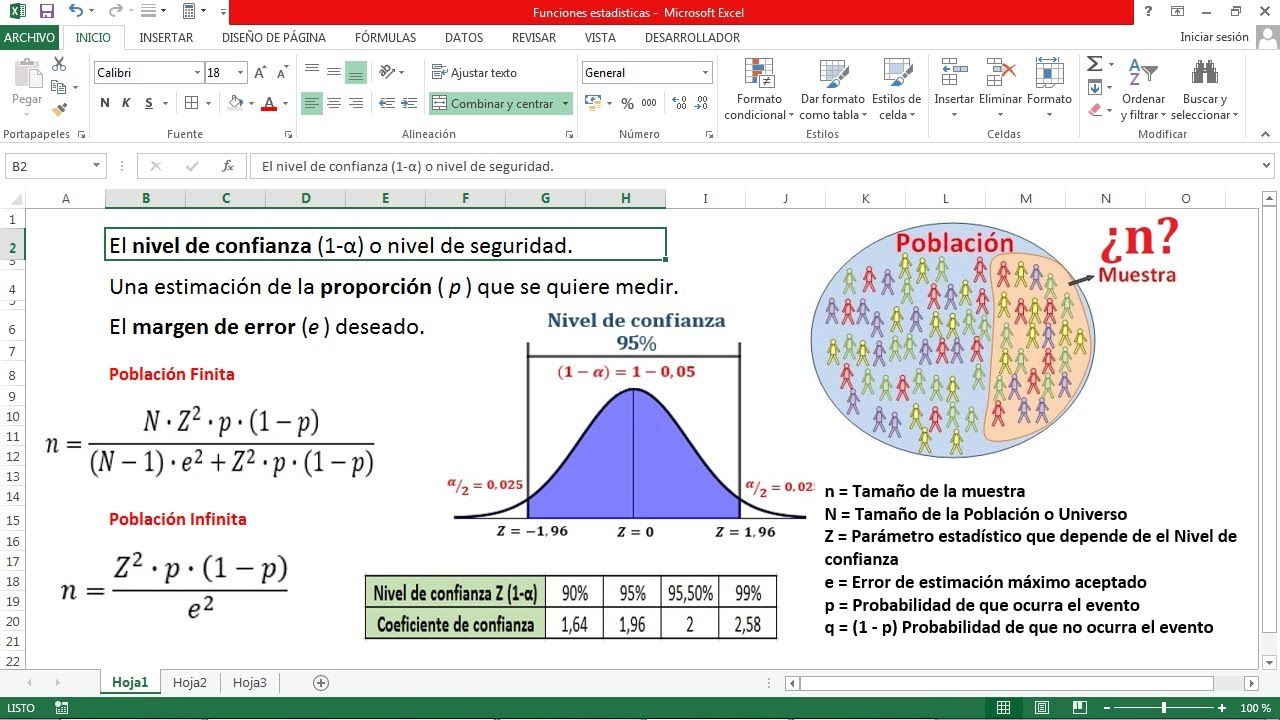
Cómo Calcular el Tamaño de la Muestra para Población Finita y Población Infinita con Excel.
5.0 / 5 (0 votes)
