Derivación implícita | Ejemplo 3
Summary
TLDRВ этом видео преподаватель объясняет процесс неявного дифференцирования, подробно разбирая пример. Он показывает, как правильно дифференцировать выражения, в которых переменные x и y перемешаны, и как использовать правило произведения и цепное правило для нахождения производной. В видео также объясняется, как изолировать производную dy/dx, чтобы выразить её через x и y. Преподаватель дает полезные советы по записи производных и предлагает зрителям дополнительную практику, чтобы закрепить материал. Видео подойдет для тех, кто изучает дифференцирование в рамках курса по математическому анализу.
Takeaways
- 😀 Введение в производные: преподаватель приветствует зрителей и напоминает о предыдущих видео по теме.
- 😀 Разница между явными и неявными производными: в неявном дифференцировании переменная 'y' не изолирована, и мы используем Δy/Δx.
- 😀 Применение правила произведения: если в выражении присутствуют обе переменные (x и y), нужно использовать правило произведения для нахождения производной.
- 😀 Правила дифференцирования: производная константы (например, 5) всегда равна 0.
- 😀 При дифференцировании произведения двух функций необходимо помнить, что применяются две части правила: первая функция умножается на производную второй, и наоборот.
- 😀 Важно добавлять Δy/Δx при дифференцировании переменной 'y'. Это необходимо для правильного отображения зависимости y от x.
- 😀 Чтобы решить задачу, нужно сначала продифференцировать все термины в уравнении, включая произведения с переменными x и y.
- 😀 После получения всех производных необходимо изолировать все термины, содержащие Δy/Δx, и перенести их на одну сторону уравнения.
- 😀 Использование факторации: после переноса всех термов на одну сторону уравнения, из Δy/Δx можно вынести общий множитель для упрощения.
- 😀 В конечном итоге, чтобы найти производную Δy/Δx, нужно разделить оставшиеся термины на общий множитель, который был вынесен.
Q & A
Что означает "деривация имплицитно"?
-Деривация имплицитно означает нахождение производной функции, где зависимость между переменными не явная, и требуется использовать правила дифференцирования для каждого термина, включая производную y относительно x.
Почему важно добавлять производную для y при дифференцировании?
-При дифференцировании y важно добавлять производную y относительно x, чтобы указать, что производная y зависит от x, а не является независимой переменной.
Какой метод используется при дифференцировании произведений?
-При дифференцировании произведений используется правило дифференцирования произведения: производная произведения двух функций равна первому множителю, умноженному на производную второго, плюс второй множитель, умноженный на производную первого.
Что происходит, если в уравнении присутствуют обе переменные x и y?
-Если в уравнении присутствуют обе переменные x и y, то они рассматриваются как множители, и при дифференцировании необходимо использовать правило произведения для правильного вычисления производной.
Какую роль играет символ с 'dy/dx' при дифференцировании?
-Символ 'dy/dx' используется для обозначения производной y относительно x, и его добавление помогает четко указать, что y является зависимой переменной от x при дифференцировании.
Почему важно следить за знаками при переносе членов уравнения?
-При переносе членов важно правильно учитывать знаки, чтобы избежать ошибок в вычислениях, так как неправильный знак может привести к неверному результату.
Что происходит, если на одном из шагов дифференцирования появляется константа?
-Если при дифференцировании появляется константа, то ее производная равна нулю, что упрощает выражение и позволяет исключить этот термин из уравнения.
Как происходит упрощение уравнений при вычислении производных?
-Упрощение уравнений происходит путем сбора всех членов, содержащих производные, с одной стороны уравнения, и остальных членов с другой стороны. Это помогает легче решить уравнение для неизвестной переменной.
Что такое 'факторизация' при решении уравнений?
-Факторизация — это процесс выделения общего множителя из всех членов, содержащих производные, чтобы упростить решение уравнения и найти производную.
Почему важно правильно выносить множители при решении уравнений?
-Правильный вынос множителей помогает упростить уравнение и изолировать производную, что облегчает дальнейшее решение уравнения.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Как начать обучение? Мой план от А1 до С1
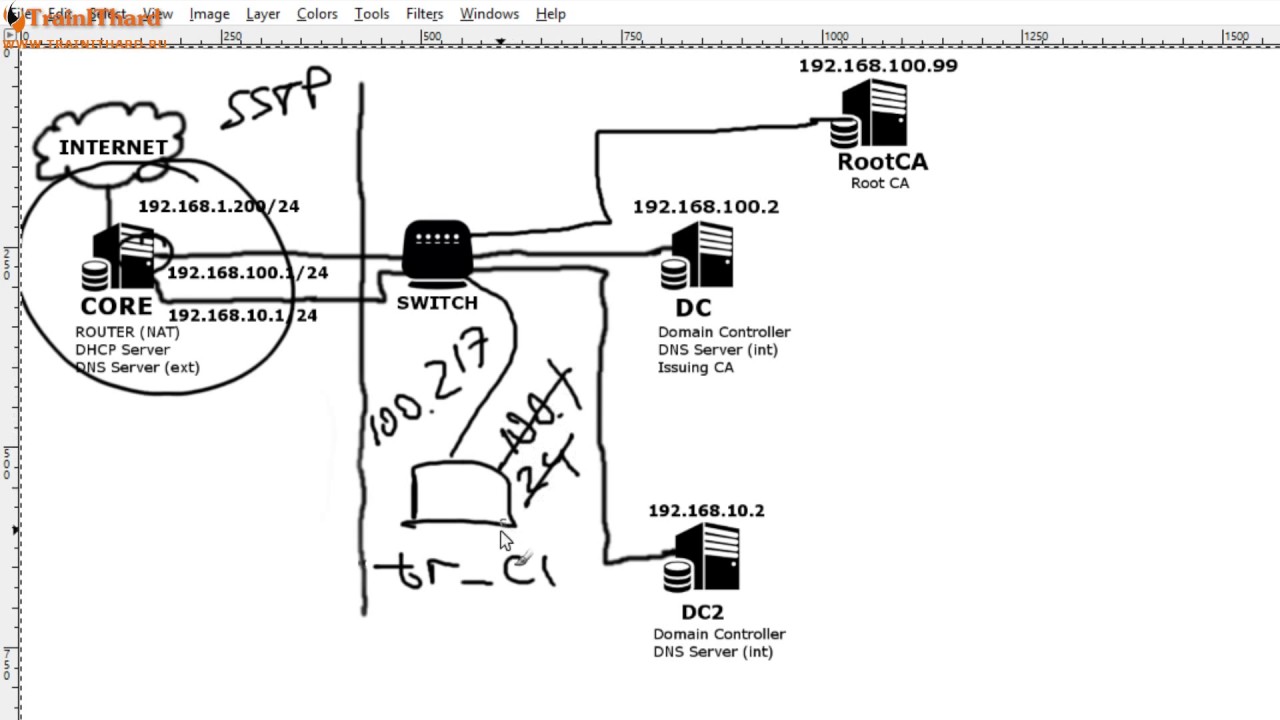
[Windows Server 2012 basics] Микроурок 11.5 - Настройка SSTP VPN

ПИЩЕВАРИТЕЛЬНАЯ СИСТЕМА человека, ферменты / ПИЩЕВАРЕНИЕ человека

🟢 Как зарабатывать ИКСЫ на премаркете? Пошаговое руководство!

The Viral AI POV Videos Masterclass – Full Course

Взрослый разговор с собой.

2年間使い倒したiPad Proはいくらで売れる?
5.0 / 5 (0 votes)