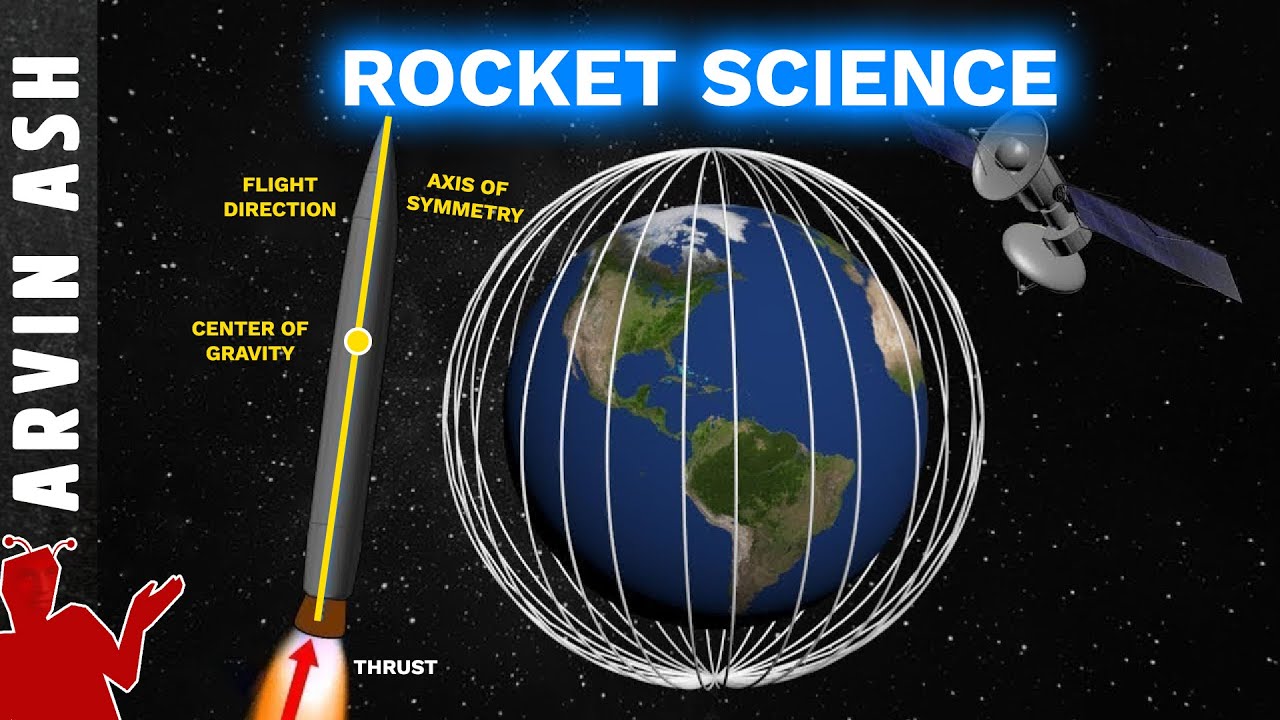
A curva que coloca FOGUETES no ESPAÇO

Summary

In this video, the narrator explores the fascinating science behind rocket launches, sparked by their experience with *Kerbal Space Program 2*. The video delves into the principles of orbital mechanics and the complexities of launching rockets efficiently. It introduces concepts like the gravity turn, a technique that minimizes fuel use by allowing gravity to guide the rocket's orientation after launch, thus reducing drag. The video explains how understanding these principles, learned through both games and real-world science, can lead to more efficient space travel. The narrator reflects on the joy of learning and the unexpected places from which knowledge can arise.

Takeaways

• 😀 Firing rockets is a fascinating and complex process, requiring careful engineering and fuel optimization.
• 😀 Rocket launches are not only a technological marvel but also involve overcoming significant challenges, such as gravity and atmospheric drag.
• 😀 Orbital mechanics is crucial for understanding how rockets achieve orbit, with speed and trajectory being the key factors.
• 😀 The ‘gravity turn’ technique is a highly efficient method of launching rockets, using gravity itself to guide the rocket’s orientation during ascent.
• 😀 The rocket launch process can be divided into vertical and horizontal components, each facing different challenges (gravity and atmospheric drag).
• 😀 Robert Goddard’s 1919 challenge, known as the ‘Goddard Problem,’ highlighted the need to optimize fuel consumption during rocket launches.
• 😀 A rocket’s trajectory must be carefully managed to balance the forces of gravity and atmospheric drag for the most efficient ascent.
• 😀 The use of a ‘gravity turn’ reduces fuel consumption by allowing the rocket to naturally adjust its orientation as it ascends.
• 😀 To achieve orbit, the rocket must reach both sufficient altitude and horizontal velocity while minimizing fuel expenditure.
• 😀 Modern rockets may not always use the exact gravity turn but still rely on optimizing the trajectory to reduce energy waste and ensure efficiency.

Q & A

What is the main challenge in rocket launches discussed in the video?

The main challenge discussed is how to efficiently launch a rocket, balancing the need to overcome gravity and atmospheric drag while conserving fuel. The video explains the problem of optimizing rocket trajectory and speed to reach orbit with minimal fuel consumption.

What is the problem of Goddard in rocket science?

The problem of Goddard, posed by Robert Goddard in 1919, involves determining the optimal rocket launch trajectory that maximizes the altitude a rocket can reach while accounting for both atmospheric drag and gravitational pull.

Why is it inefficient to launch a rocket vertically to reach orbit?

Launching a rocket vertically requires significant fuel to overcome gravity, and much of this fuel is wasted on altitude gain rather than building the necessary horizontal speed for orbit. This makes vertical launches an inefficient way to enter orbit.

How does the Earth's atmosphere impact rocket launches?

The atmosphere creates drag that resists the rocket's motion. As the rocket speeds up, the drag increases, requiring more fuel to maintain acceleration. The rocket's trajectory must balance this drag with the need to gain horizontal speed to enter orbit.

What is the gravitational curve (gravity turn) in rocket launches?

The gravitational curve is a technique used during rocket launches where the rocket gradually tilts its trajectory, allowing gravity to assist in aligning the rocket’s direction with its motion. This helps minimize fuel use and optimize the launch trajectory.

How does gravity assist in the efficiency of rocket launches?

Gravity helps by gradually altering the rocket's orientation during the launch. As the rocket moves upward and accelerates, gravity pulls it to a more horizontal orientation, which helps reduce atmospheric drag and optimize fuel efficiency.

Why is the alignment of the rocket's trajectory important during launch?

Maintaining proper alignment is crucial because a misalignment would increase the atmospheric drag on the rocket. The goal is to keep the rocket’s orientation in line with its movement to minimize energy loss and maximize fuel efficiency.

What is the role of the rocket's angle of attack during launch?

The angle of attack is the angle between the rocket’s trajectory and the direction of motion. A small angle of attack is ideal as it minimizes drag, preventing fuel wastage and helping the rocket move more efficiently through the atmosphere.

What makes a gravitational curve more efficient than a vertical launch?

A gravitational curve is more efficient because it uses gravity to gradually adjust the rocket’s orientation, reducing the need for additional fuel to adjust the rocket's trajectory. This helps conserve fuel while achieving the necessary horizontal speed to enter orbit.

How does the concept from the game Kerbal Space Program 2 relate to real-world rocket science?

In the game Kerbal Space Program 2, players simulate rocket launches, learning about the complexities of fuel management, orbital mechanics, and trajectory planning. The game inspired the creator of the video to explore real-world rocket science, particularly optimizing fuel use and understanding orbital mechanics.