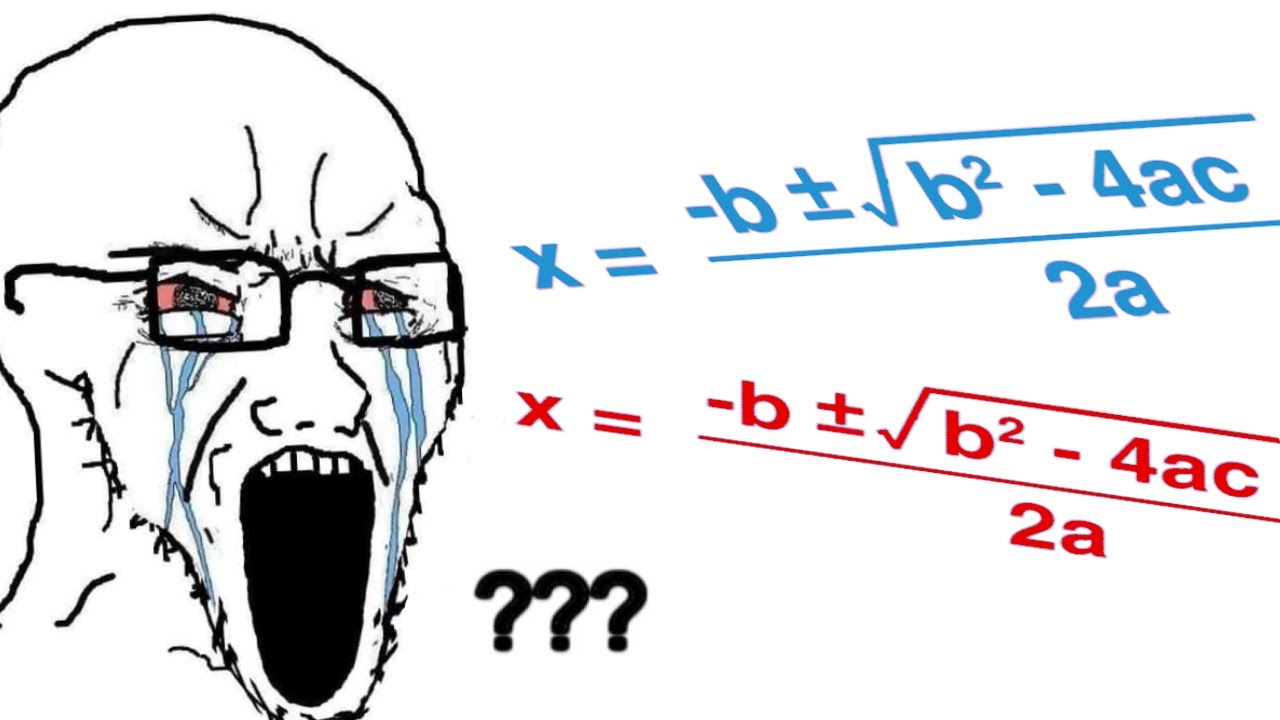GRINGS - Equações Diferenciais Ordinárias - Aula 1
Summary
TLDRThis video provides a comprehensive introduction to differential equations, starting with the basics of algebraic equations and gradually moving into more complex topics. It explains the difference between algebraic equations (like linear and quadratic) and differential equations, which involve functions and their derivatives. The video covers key concepts such as the order and degree of differential equations, their classification into ordinary and partial types, and the process of solving them by verifying potential solutions. The goal is to help viewers understand the foundational aspects of differential equations and how to approach solving them.
Takeaways
- 😀 Equations are mathematical equalities, such as x = 4 in a simple linear equation. Solving an equation means finding the value of the unknown variable.
- 😀 A quadratic equation involves a second-degree term, and its solutions can be positive or negative, as demonstrated by x = ±3.
- 😀 Exponential equations have the variable in the exponent, such as x^2 = 9, where x = 3 or x = -3 is the solution.
- 😀 Differential equations involve a function and its derivatives, such as y' - y = 0, where y is the unknown function and its derivatives appear in the equation.
- 😀 Ordinary differential equations (ODEs) depend on only one independent variable, while partial differential equations (PDEs) depend on more than one independent variable.
- 😀 The order of a differential equation is determined by the highest derivative appearing in the equation. For example, if the highest derivative is the second, it is a second-order equation.
- 😀 The degree of a differential equation is the exponent of the highest-order derivative when the equation is written as a polynomial.
- 😀 To solve a differential equation, a solution must satisfy both the equation and its derivatives, as illustrated with specific function examples.
- 😀 A solution to a differential equation is verified by substituting the function and its derivatives back into the equation to check for equality.
- 😀 The process of verifying solutions often involves calculating derivatives and checking if both sides of the equation balance. For example, checking if y = e^2x satisfies the equation y' = e^2x.
- 😀 Not every proposed function is a solution to a differential equation, as shown when checking y = 1 for the given equation. It failed to satisfy the equation and is not a solution.
Q & A
What is the definition of an equation?
-An equation is a mathematical expression where two terms are set equal to each other, often involving variables and constants. For example, equations like '3x + 12 = 24' or 'x^2 + 5x + 6 = 0' are typical examples.
What distinguishes a differential equation from a regular equation?
-A differential equation involves a function and its derivatives, while a regular equation only involves variables and constants. For example, the equation 'y' - 'y' = 0, with a derivative term, is a differential equation.
What does the term 'order' mean in the context of a differential equation?
-The order of a differential equation refers to the highest derivative of the function that appears in the equation. For instance, if the highest derivative is the second derivative, the order of the equation is 2.
How is the 'degree' of a differential equation defined?
-The degree of a differential equation refers to the highest power of the highest order derivative. For example, if the second derivative is raised to a power of 3, the degree of the equation is 3.
What is an ordinary differential equation (ODE)?
-An ordinary differential equation (ODE) involves a function of one independent variable and its derivatives. For example, equations like 'y' - y' = 0 or '3y' + 4y = 3 are ODEs.
What is a partial differential equation (PDE)?
-A partial differential equation (PDE) involves a function of more than one independent variable and its partial derivatives. It is used to model phenomena that depend on multiple variables, such as temperature distribution in a two-dimensional space.
What is the purpose of solving a differential equation?
-The purpose of solving a differential equation is to find a function that satisfies both the equation and its derivatives, effectively describing a relationship between the function and its rate of change over time or space.
How do you verify if a function is a solution to a differential equation?
-To verify if a function is a solution to a differential equation, you substitute the function and its derivatives into the equation and check if both sides of the equation are equal.
Can you give an example of verifying a solution to a differential equation?
-For the equation 'y' - y' = 0, if the function is y = e^(2x), its derivative y' = 2e^(2x). Substituting into the equation gives e^(2x) - 2e^(2x) = 0, which satisfies the equation, confirming it as a solution.
What are the main differences between an ODE and a PDE?
-An ODE (Ordinary Differential Equation) involves only one independent variable, while a PDE (Partial Differential Equation) involves two or more independent variables. ODEs typically model simpler systems, while PDEs are used to model more complex, multidimensional phenomena.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)