📈 Relazioni degli insiemi e proprietà - simmetrica e anti, riflessiva e anti, transitiva + esempi 🤓💻
Summary
TLDRThis video explores the relationships between sets, defining how elements from one set can be associated with elements in another. Key concepts include the domain and image of a relation, as well as various properties of relations such as reflexive, symmetric, transitive, antireflexive, and antisymmetric. Through clear examples and visual representations, the speaker illustrates these definitions, making them accessible and engaging. Viewers are encouraged to deepen their understanding by practicing these concepts.
Takeaways
- 😀 A relation between two sets A and B associates elements of A with one or more elements of B.
- 😀 The domain of a relation consists of all elements in the first set that have at least one corresponding element in the second set.
- 😀 The image of a relation is the set of all elements in the second set that are related to at least one element in the first set.
- 😀 A binary relation occurs when both the starting and arriving sets are the same.
- 😀 A relation is reflexive if every element is related to itself.
- 😀 A relation is symmetric if, whenever one element is related to another, the reverse is also true.
- 😀 A relation is transitive if, whenever one element is related to a second, and that second is related to a third, the first is also related to the third.
- 😀 An antireflexive relation has no element related to itself.
- 😀 A relation is antisymmetric if, for any two elements where one is related to the other, the reverse does not hold.
- 😀 Understanding these properties helps to classify relations and better understand their structures.
Q & A
What is a relation between two sets?
-A relation between two sets A and B is a process that associates elements from set A to one or more elements in set B.
How is the domain of a relation defined?
-The domain of a relation is the set of all elements in the first set (A) that have at least one corresponding element in the second set (B).
What constitutes the image of a relation?
-The image of a relation is the set formed by all elements in the second set (B) that are images of at least one element from the first set (A).
What is a binary relation?
-A binary relation is a relation in which both the starting set and the arriving set are the same, leading to relations among the elements of a single set.
What does it mean for a relation to be reflexive?
-A relation is reflexive if every element in the set is related to itself.
Can you explain the symmetric property of relations?
-A relation is symmetric if, whenever one element is related to another, the second element is also related back to the first.
What is the definition of transitive relations?
-A relation is transitive if, whenever an element x is related to y and y is related to z, then x is also related to z.
What characterizes an antireflexive relation?
-A relation is antireflexive if no element in the set is related to itself.
What does it mean for a relation to be antisymmetric?
-A relation is antisymmetric if, whenever one element is related to another, the reverse relationship does not hold, meaning if x is related to y, y cannot be related to x.
Why is understanding these properties important?
-Understanding these properties is crucial for analyzing relationships in mathematics, particularly in set theory, as they help define how elements interact within sets.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Representações de Conjuntos - AULA 1 - Curso de Conjuntos - Professora Angela

Introduction to Sets || Mathematics in the Modern World
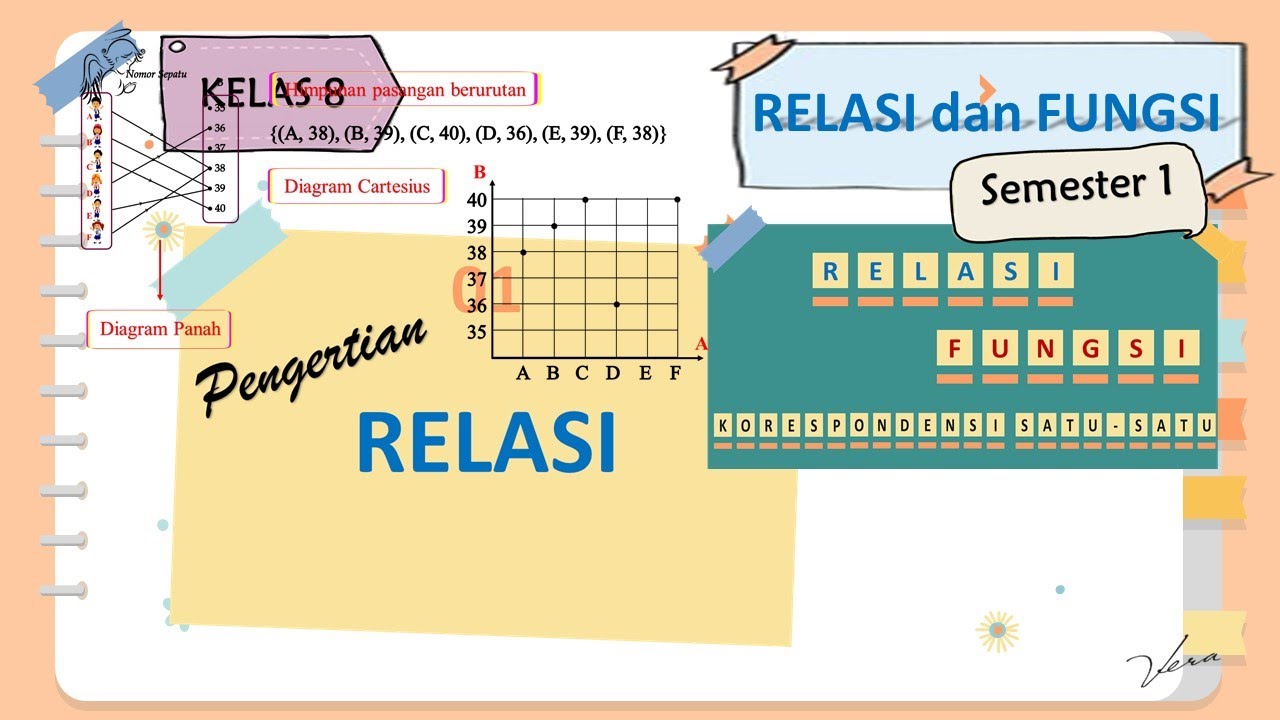
1 PENGERTIAN RELASI - RELASI DAN FUNGSI - KELAS 8 SMP

Kalkulus Part. 6 - Fungsi dan Jenisnya, Daerah asal dan Daerah Hasil

Operations on Sets (Tagalog/Filipino Math)

Set Operations
5.0 / 5 (0 votes)
