Física: Ley de Gauss - Traful
Summary
TLDREl profesor Miranda, de la UTEM, presenta un video educativo sobre la Ley de Gauss, fundamental en la física para determinar el campo eléctrico en distribuciones de carga complejas. Explica cómo esta ley simplifica los cálculos al utilizar una superficie gaussiana cerrada que facilita la evaluación del flujo eléctrico en función de la carga encerrada. Mediante ejemplos, ilustra su aplicación en diferentes configuraciones de carga como esferas, cilindros y planos infinitos, destacando la importancia de la simetría en estas situaciones para resolver problemas de campo eléctrico de manera eficiente.
Takeaways
- 😀 La Ley de Gauss es útil para determinar el campo eléctrico en sistemas con cargas puntuales y distribuciones continuas de carga.
- 📚 El método tradicional para calcular campos eléctricos puede ser complejo; la Ley de Gauss ofrece una alternativa más simple bajo ciertas condiciones.
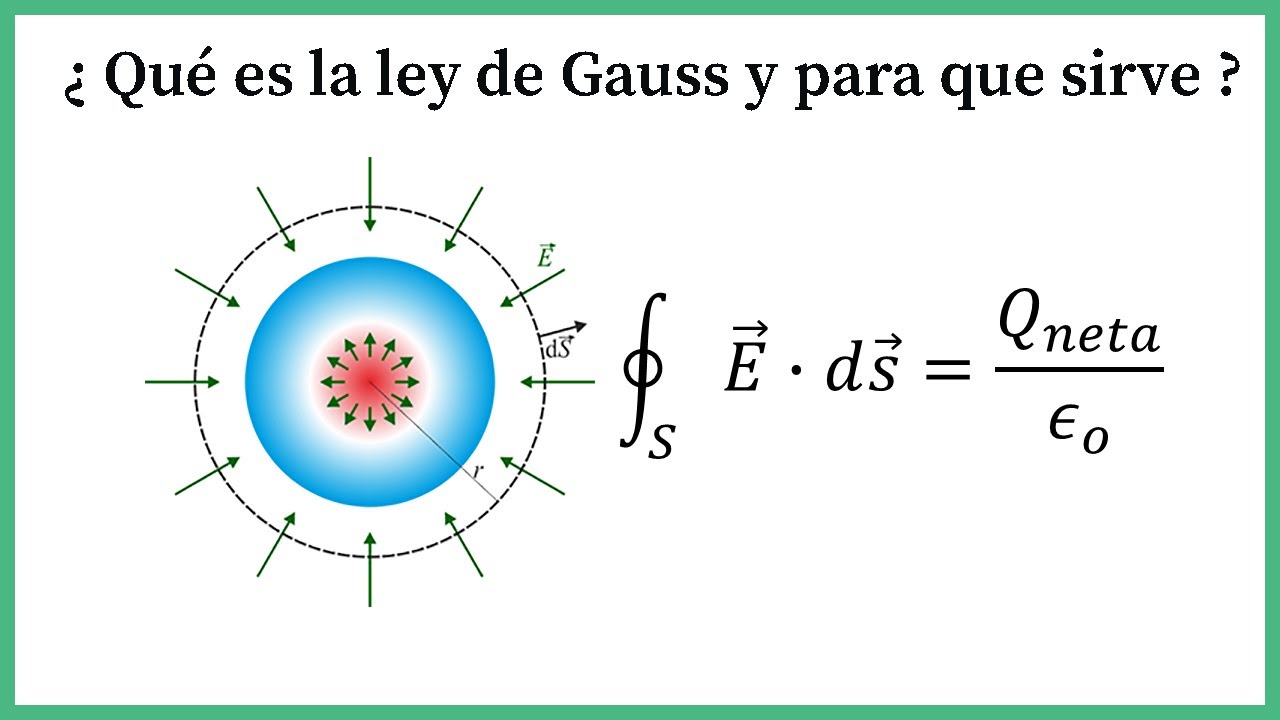
- 🔍 La Ley de Gauss establece que el flujo eléctrico a través de una superficie cerrada es proporcional a la carga encerrada dentro de esa superficie.
- 🧐 Esta ley es especialmente útil en casos con alto grado de simetría en la distribución de carga, como planos grandes, esferas y cilindros largos cargados.
- 🔬 Para aplicar la Ley de Gauss, primero se selecciona una superficie gaussiana adecuada basada en la simetría de la distribución de carga.
- ✅ El flujo eléctrico se calcula como el producto de la magnitud del campo eléctrico y el área diferencial, orientado normalmente a la superficie.
- ⚖️ Ejemplos específicos incluyen la determinación del campo eléctrico dentro y fuera de un cascarón esférico y alrededor de un alambre infinitamente largo.
- 📐 En el caso de una esfera con una carga positiva, el campo eléctrico dentro es cero, mientras que fuera es inversamente proporcional al cuadrado de la distancia desde el centro.
- 📏 Para un alambre infinitamente largo, el campo eléctrico se calcula usando una superficie cilíndrica gaussiana y es inversamente proporcional al radio.
- 📖 En el caso de una lámina plana e infinita con carga uniforme, el campo eléctrico resultante es constante y depende directamente de la densidad superficial de carga.
Q & A
¿Qué es la ley de Gauss y cuál es su utilidad?
-La ley de Gauss establece que el flujo eléctrico a través de una superficie cerrada es proporcional a la carga neta encerrada por dicha superficie. Su utilidad radica en simplificar el cálculo del campo eléctrico en situaciones de alta simetría en la distribución de carga.
¿Cómo se calcula el flujo eléctrico según la ley de Gauss?
-El flujo eléctrico se calcula multiplicando la magnitud del campo eléctrico en un punto por el área de la superficie Gaussiana, y luego multiplicando por el coseno del ángulo entre el campo eléctrico y el vector normal a la superficie.
¿Cuándo se utiliza la ley de Gauss?
-Se utiliza principalmente en situaciones donde existe un alto grado de simetría en la distribución de carga, como en el caso de cargas esféricas, planos infinitos y cilindros infinitamente largos.
¿Cuál es el primer paso para determinar el campo eléctrico utilizando la ley de Gauss?
-El primer paso es seleccionar la superficie Gaussiana adecuada, lo cual se realiza en función de la geometría de la carga.
¿Qué condiciones deben cumplirse para utilizar la ley de Gauss en un problema?
-La ley de Gauss se aplica cuando existe simetría en la distribución de carga, es decir, cuando los vectores del campo eléctrico y el vector normal a la superficie Gaussiana son paralelos o perpendiculares.
¿Cómo se elige la superficie Gaussiana?
-La elección de la superficie Gaussiana se realiza en función de la geometría de la carga. Para distribuciones esféricas se elige una superficie esférica, mientras que para planos infinitos y cilindros infinitamente largos se elige una superficie cilíndrica.
¿Cuál es el segundo paso para determinar el campo eléctrico usando la ley de Gauss?
-El segundo paso consiste en determinar cuánta de la carga total está encerrada por la superficie Gaussiana seleccionada.
¿Cómo se calcula el campo eléctrico una vez determinada la carga encerrada?
-Una vez determinada la carga encerrada por la superficie Gaussiana, se utiliza la ley de Gauss para igualar el flujo eléctrico al cociente entre la carga encerrada y la constante dieléctrica.
¿Qué es el flujo eléctrico neto a través de una superficie Gaussiana?
-El flujo eléctrico neto es la suma de los flujos eléctricos entrantes y salientes a través de una superficie Gaussiana, siendo positivo si hay una cantidad neta de carga positiva encerrada y negativo si hay una cantidad neta de carga negativa encerrada.
¿Cuál es la fórmula para calcular el campo eléctrico en una distribución uniforme de carga a lo largo de un alambre delgado infinito?
-El campo eléctrico se calcula utilizando la ley de Gauss y la carga por unidad de longitud del alambre. La fórmula es E = (k * lambda) / r, donde lambda es la carga por unidad de longitud, k es la constante electrostática y r es la distancia al alambre.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

35. Ley de Gauss- Ejercicio basico para comprender
34. Ley de Gauss Explicación-Todo lo que debes saber

44. Campo eléctrico generado por un hilo cargado infinito- Ley de Gauss

Calcular intensidad de campo eléctrico - Ejercicio resuelto, fórmula y definición

Clase 11: Concepto del Campo Eléctrico para una carga puntual y un conjunto discreto.

⚡ Campo Eléctrico | Video 8
5.0 / 5 (0 votes)
