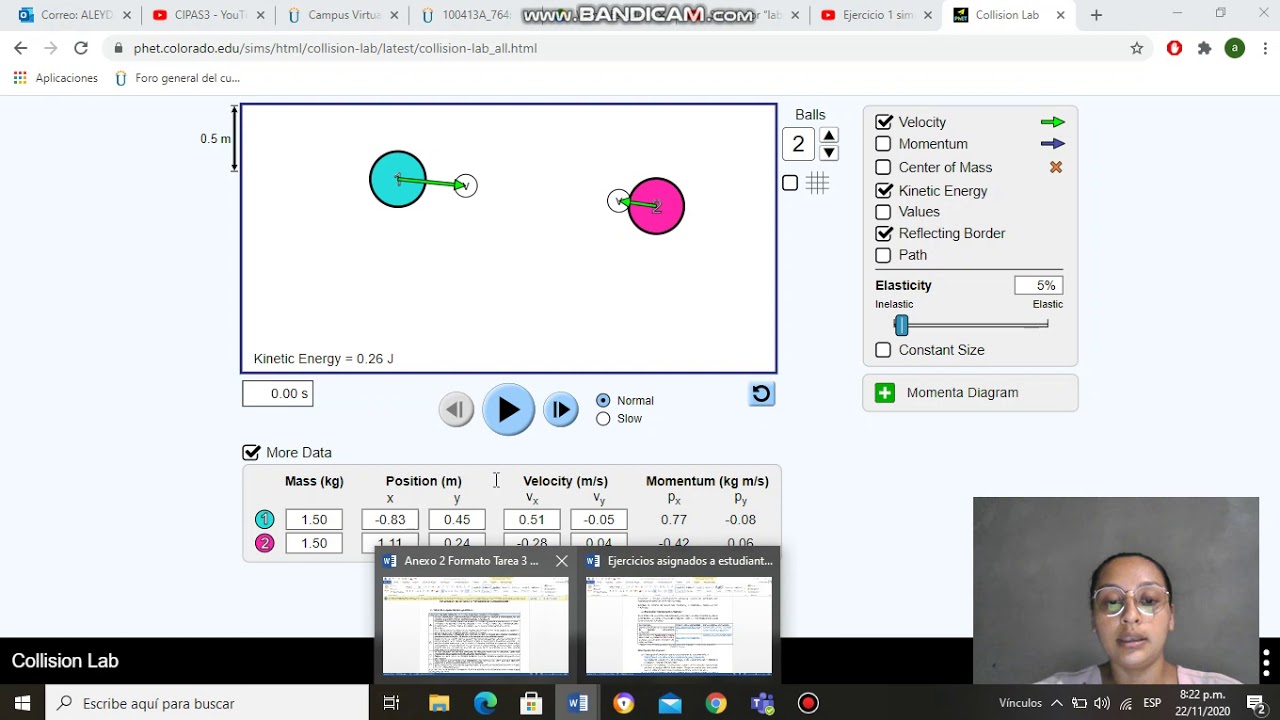
Cómo calcular la velocidad en una colisión elástica (2 bolas en movimiento) - Ejercicio Avanzado

Física para todos

10 Aug 202320:34

Summary

TLDREn este video, se resuelve un ejercicio de colisiones elásticas entre dos esferas de diferente masa y velocidad. A través de los principios de conservación de la cantidad de movimiento y de la energía cinética, se calcula la velocidad final de ambas esferas después del choque. Se explica paso a paso cómo plantear y resolver las ecuaciones necesarias para obtener las soluciones, incluyendo la aplicación de la fórmula cuadrática para determinar las velocidades finales. El ejercicio es avanzado y busca ayudar a los estudiantes a comprender de manera clara cómo resolver este tipo de problemas de física.

Takeaways

😀 Se trata de un ejercicio de colisiones o choques elásticos entre dos esferas en movimiento.
😀 El objetivo es calcular la velocidad final de ambas esferas después de la colisión.
😀 Se introduce la conservación de la cantidad de movimiento (impulso) y la conservación de la energía cinética como principios clave para resolver el problema.
😀 La primera esfera tiene una masa de 1 kg y una velocidad inicial de 2,2 m/s en la dirección positiva del eje x.
😀 La segunda esfera tiene una masa de 1,5 kg y una velocidad inicial de -3 m/s (en dirección negativa del eje x).
😀 Se plantean dos ecuaciones fundamentales: la conservación de la cantidad de movimiento y la conservación de la energía cinética.
😀 Se aplica la fórmula de la cantidad de movimiento, tomando en cuenta las masas y las velocidades iniciales y finales de las esferas.
😀 La ecuación de conservación de la energía cinética se usa para relacionar las velocidades iniciales y finales de las esferas, eliminando el factor 1/2 en ambos lados.
😀 Al resolver las ecuaciones, se obtienen dos incógnitas, lo que requiere un sistema de ecuaciones para hallar las velocidades finales.
😀 Después de resolver la ecuación cuadrática, se obtiene una solución negativa (-3,0 m/s) y una positiva (1,16 m/s) para la velocidad final de la segunda bola.
😀 Se selecciona la solución positiva (1,16 m/s) para la velocidad final de la bola 2, ya que la negativa no tiene sentido físico en este contexto.
😀 Finalmente, se calcula la velocidad final de la bola 1 usando la velocidad final de la bola 2 y se obtiene un valor de -0,4 m/s, indicando que la bola 1 se mueve en la dirección negativa del eje x.

Q & A

¿Qué tipo de colisión se está analizando en el ejercicio?
-Se está analizando una colisión elástica, en la cual se conservan tanto la cantidad de movimiento como la energía cinética.
¿Cuáles son las masas de las dos bolas involucradas en la colisión?
-La primera bola tiene una masa de 1 kg, y la segunda bola tiene una masa de 1,5 kg.
¿Cuál es la velocidad de la bola 1 antes de la colisión?
-La velocidad de la bola 1 antes de la colisión es de 2,2 m/s en la dirección positiva del eje x.
¿En qué dirección se mueve la bola 2 antes de la colisión?
-La bola 2 se mueve en la dirección negativa del eje x con una velocidad de -3 m/s.
¿Qué principios se utilizan para resolver el ejercicio?
-Se utilizan los principios de conservación de la cantidad de movimiento (o momentum) y conservación de la energía cinética.
¿Cómo se define la cantidad de movimiento (p) en este ejercicio?
-La cantidad de movimiento se define como el producto de la masa por la velocidad, es decir, p = m * v.
¿Por qué no se pueden usar las ecuaciones previas para resolver este ejercicio?
-Las ecuaciones previas no sirven porque se derivaron cuando una de las esferas estaba en reposo, y este ejercicio involucra dos esferas en movimiento.
¿Cómo se resuelve el sistema de ecuaciones planteado para encontrar las velocidades finales?
-Se plantean dos ecuaciones, una para la conservación de la cantidad de movimiento y otra para la conservación de la energía cinética. Luego, se resuelven simultáneamente para obtener las velocidades finales de las dos bolas.
¿Qué ocurre con la solución negativa obtenida para la velocidad final de la bola 2?
-La solución negativa para la velocidad final de la bola 2, que es de -3 m/s, se descarta porque no tiene sentido físico en este contexto, ya que implica que la bola 2 se detendría en el mismo lugar donde estaba inicialmente.
¿Qué significa el signo negativo en la velocidad final de la bola 1?
-El signo negativo en la velocidad final de la bola 1 indica que la bola 1 se mueve en la dirección negativa del eje x después de la colisión, es decir, en la dirección opuesta a su movimiento inicial.