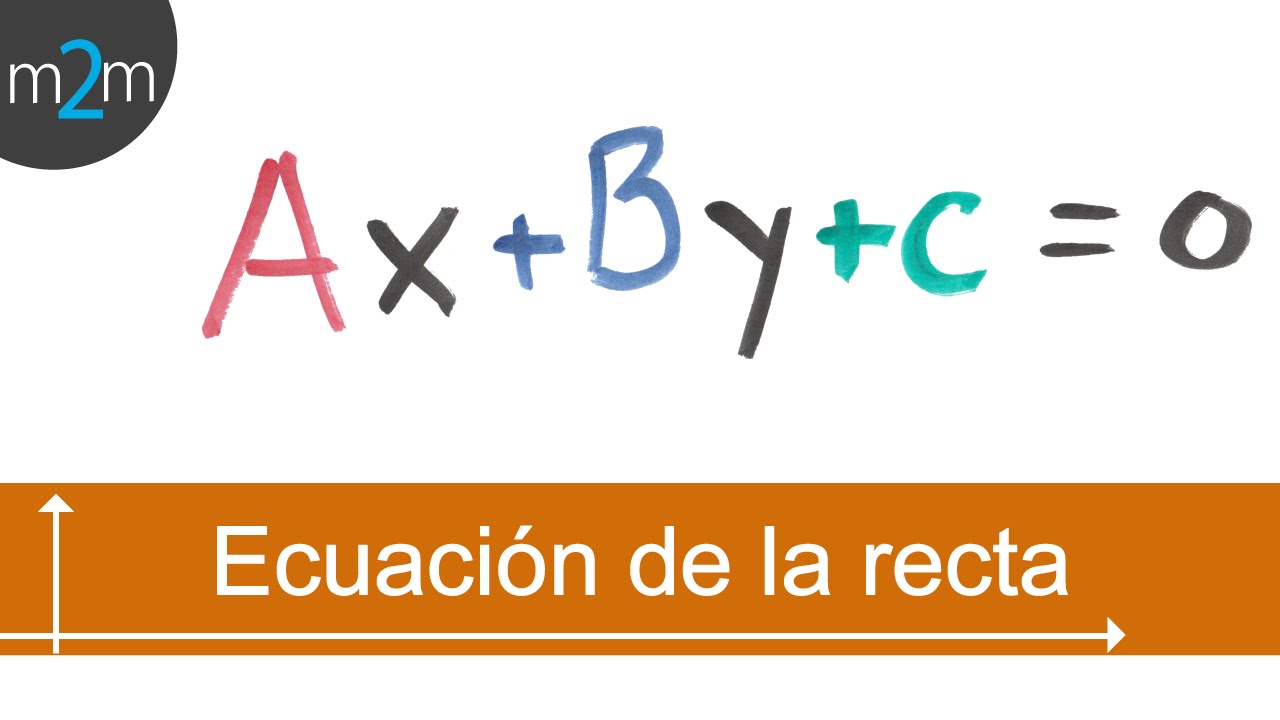Ecuaciones de la recta y sus transformaciones
Summary
TLDREn este video, se explica cómo trabajar con ecuaciones de la recta y sus transformaciones, utilizando diferentes formas, como la ecuación general y la forma punto-pendiente. Se detallan los pasos para calcular la pendiente, la abscisa al origen y la ordenada al origen, mediante ejemplos prácticos. El proceso incluye la sustitución de coordenadas en las fórmulas correspondientes, pasando de una forma a otra hasta obtener la ecuación final. A lo largo del ejercicio, se hace énfasis en la importancia de entender y aplicar las fórmulas de manera precisa para resolver problemas de rectas y sus transformaciones.
Takeaways
- 😀 La ecuación de la recta puede ser expresada usando dos puntos y la fórmula general, donde se sustituyen los valores de las coordenadas para encontrar la ecuación de la recta.
- 😀 La fórmula básica para la ecuación de una recta a partir de dos puntos es: (y - y1) = ((y2 - y1) / (x2 - x1)) * (x - x1).
- 😀 Se debe calcular la pendiente (m) primero, utilizando los valores de los puntos dados. En este caso, la pendiente resultó ser m = 3.
- 😀 Tras calcular la pendiente, se puede usar la fórmula de punto-pendiente para obtener la ecuación de la recta: y - y1 = m * (x - x1).
- 😀 En este caso, la ecuación de la recta derivada de los puntos dados fue simplificada a la forma general: 3x - 6 - y = -5.
- 😀 La forma general de la recta puede reordenarse para obtener una ecuación más sencilla: 3x - y - 5 = 0.
- 😀 Para convertir la ecuación de la recta a la forma pendiente-ordenada al origen, se despejan los términos adecuados, resultando en y = 3x - 5.
- 😀 Para calcular la ordenada al origen (b), se puede despejar de la ecuación general o utilizar la fórmula, resultando en b = -5.
- 😀 La abscisa al origen (la intersección de la recta con el eje X) se calcula utilizando la fórmula x = -c / a, obteniendo el valor x = 5/3.
- 😀 El proceso también puede utilizarse para encontrar la ecuación de la recta en su forma general a partir de la forma canónica o asimétrica.
Q & A
¿Cuál es la ecuación de la recta cuando se da por dos puntos?
-La ecuación de la recta cuando se da por dos puntos se expresa como: (y - y1) = m(x - x1), donde m es la pendiente, calculada como (y2 - y1) / (x2 - x1).
¿Cómo se calcula la pendiente de la recta?
-La pendiente (m) de la recta se calcula como la diferencia de las coordenadas y entre los dos puntos, dividida entre la diferencia de las coordenadas x: m = (y2 - y1) / (x2 - x1).
¿Qué se hace después de calcular la pendiente para obtener la ecuación en la forma general?
-Una vez calculada la pendiente, se sustituye en la fórmula de la ecuación de la recta y se despeja para obtener la forma general, que es: Ax + By + C = 0.
¿Cómo se obtiene la forma general de la ecuación después de usar la fórmula punto-pendiente?
-Para obtener la forma general, se multiplica la ecuación punto-pendiente por la pendiente y se reordenan los términos para tener la variable x y la variable y de un lado y un constante del otro lado, finalmente se iguala a cero.
¿Qué significa la ordenada al origen en el contexto de las ecuaciones de la recta?
-La ordenada al origen es el valor de y cuando x es igual a cero, es decir, el punto en el que la recta corta el eje y.
¿Cómo se encuentra la ordenada al origen usando la ecuación en forma general?
-Para encontrar la ordenada al origen, se sustituye x = 0 en la ecuación de la recta y se resuelve para y, lo que da el valor de la intersección con el eje y.
¿Cómo se obtiene la abscisa al origen?
-La abscisa al origen es el valor de x cuando y es igual a cero. Se encuentra sustituyendo y = 0 en la ecuación de la recta y resolviendo para x.
¿Qué forma tiene la ecuación de la recta cuando se expresa en forma pendiente-intersección?
-La forma pendiente-intersección de la ecuación de la recta es: y = mx + b, donde m es la pendiente y b es la ordenada al origen.
¿Qué es la forma canónica o asimétrica de una ecuación de la recta?
-La forma canónica o asimétrica de la ecuación de la recta se refiere a una versión de la ecuación que involucra fracciones, y se usa para representar la ecuación de forma diferente a la forma general o pendiente-intersección.
¿Qué procedimiento se debe seguir si no se conocen los valores de la pendiente y la ordenada al origen?
-Si no se conocen los valores de la pendiente y la ordenada al origen, se pueden calcular utilizando la fórmula de la pendiente a partir de dos puntos dados y luego derivar la ecuación en forma general a partir de la fórmula punto-pendiente.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)