Double Integral, definition as Double Riemann Sum, FULL EXPLANATION
Summary
TLDREn este video, se explica cómo calcular el volumen debajo de una superficie definida por una función de dos variables. Se parte de un rectángulo que se divide en subrectángulos más pequeños, utilizando la suma de volúmenes de prismas para aproximar el volumen total. Se enfatiza la importancia de seleccionar un punto específico dentro de cada rectángulo para determinar la altura del prisma, y se presenta cómo, al llevar las particiones a infinito, se puede representar el volumen como una integral doble. Este enfoque formaliza la comprensión del volumen bajo una superficie en múltiples dimensiones.
Takeaways
- 😀 La gráfica representa una función de dos variables, xy.
- 😀 Se busca calcular el volumen sobre un rectángulo dividiéndolo en sub-rectángulos más pequeños.
- 😀 El volumen de un prisma se calcula como el área de la base multiplicada por la altura.
- 😀 La altura se determina evaluando la función en un punto específico dentro del rectángulo.
- 😀 Se utilizan subíndices (i y j) para identificar la posición de los rectángulos en ambas direcciones.
- 😀 El área de la base del prisma se determina a partir de los intervalos de las variables x y y.
- 😀 La suma de los volúmenes de todos los prismas se utiliza para aproximar el volumen total bajo la superficie.
- 😀 La notación sigma se emplea para abreviar la suma de volúmenes de los prismas en cada columna.
- 😀 A medida que el número de intervalos (n y m) tiende a infinito, los prismas se vuelven más delgados y la aproximación mejora.
- 😀 El concepto de límite es fundamental para definir el volumen bajo la superficie mediante una integral doble.
Q & A
¿Cuál es el objetivo principal de la gráfica mencionada en el video?
-El objetivo principal es calcular el volumen por encima de un rectángulo bajo la superficie de una función de dos variables.
¿Cómo se divide el rectángulo inicial para facilitar el cálculo del volumen?
-El rectángulo se divide en varios rectángulos más pequeños, dividiendo los intervalos en múltiples partes más pequeñas para obtener prismas.
¿Qué fórmula se utiliza para calcular el volumen de un prisma?
-La fórmula es el volumen igual al área de la base por la altura del prisma.
¿Cómo se elige el punto para calcular la altura del prisma?
-Se elige un punto dentro de cada rectángulo, cuya coordenada se expresa como (xᵢ, yⱼ), para evaluar la función y determinar la altura.
¿Qué significa el asterisco (*) en la notación de la función?
-El asterisco indica que se está seleccionando un punto específico en lugar de referirse a todos los puntos dentro del rectángulo.
¿Qué se utiliza para calcular el área de la base del prisma?
-El área de la base se calcula multiplicando los intervalos Δx y Δy, que representan las longitudes de los lados del rectángulo.
¿Cómo se representa la suma de los volúmenes de los prismas?
-Se utiliza notación sigma para abreviar la suma de los volúmenes de los prismas, facilitando el manejo de las sumas de múltiples rectángulos.
¿Qué sucede con los valores de n y m para mejorar la aproximación del volumen?
-Los valores de n y m tienden a infinito, lo que hace que los rectángulos sean cada vez más pequeños y mejora la aproximación del volumen bajo la superficie.
¿Cuál es el resultado final al aplicar el límite de las sumas?
-El resultado final se expresa como una integral doble, que formaliza el volumen debajo de la superficie de la función de dos variables.
¿Por qué es importante el apoyo de la comunidad según el presentador?
-El presentador destaca la importancia del apoyo comunitario para la creación de contenido educativo, agradeciendo a quienes contribuyen a su trabajo en plataformas como YouTube y Patreon.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Análisis Matemático II - Teorema Fundamental de Cálculo Integral - Parte 3

Cálculo Integral - Tutorial de Área bajo la curva
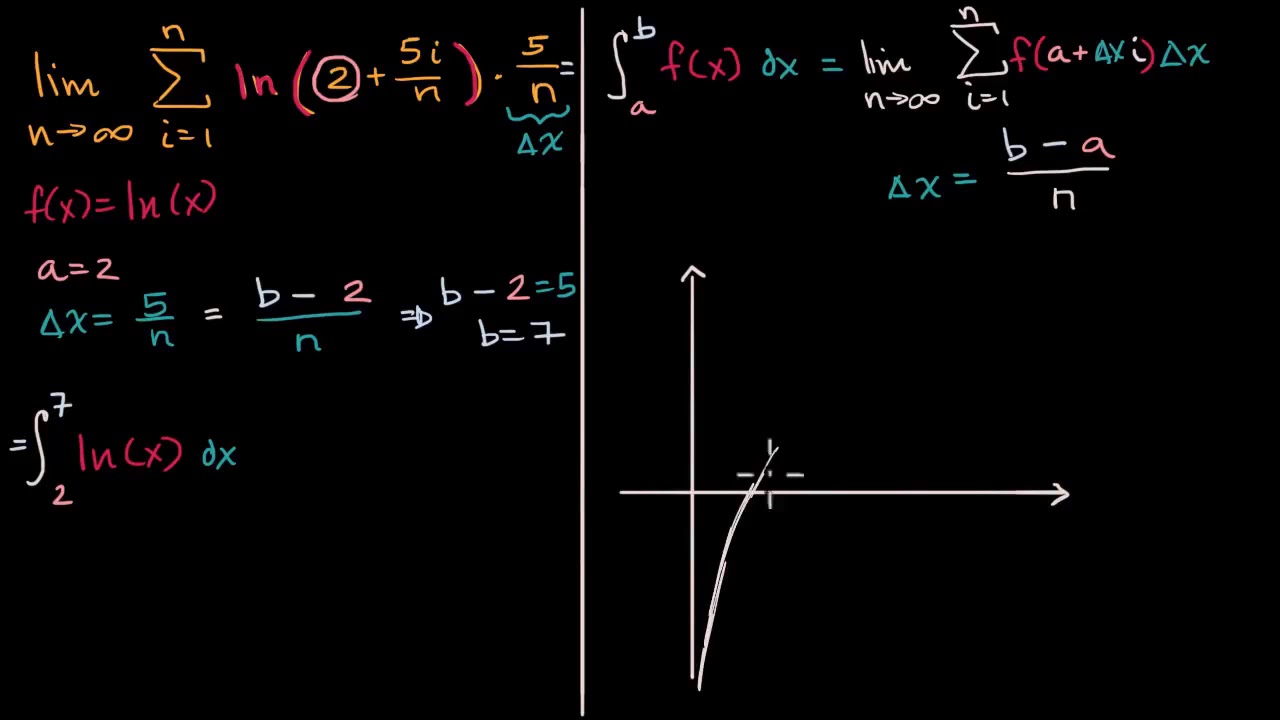
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Calculo de Área de una región plana

Fourier series WITH GRAPHIC, VERY EASY
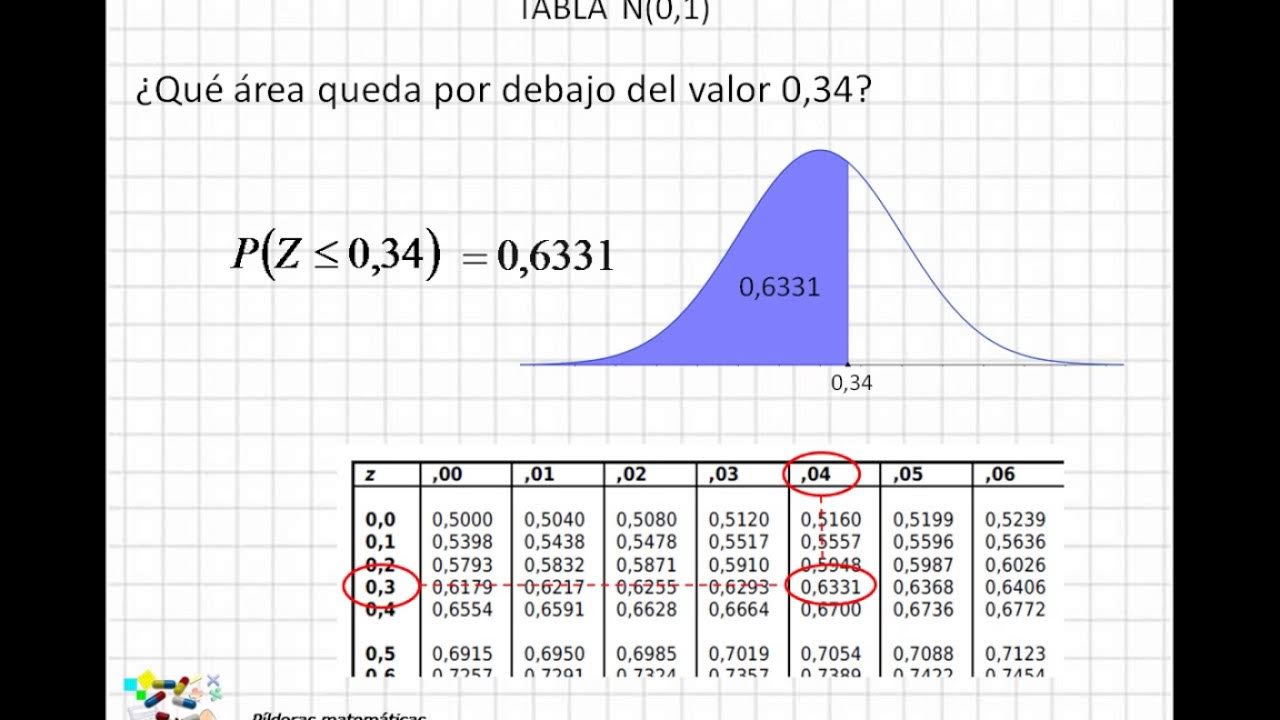
04 Cómo usar la tabla de distribución normal
5.0 / 5 (0 votes)
