What is Multiplication?
Summary
TLDRIn this insightful discussion, the speaker explores the complexities and nuances of multiplication, particularly regarding negative numbers and fractions. They highlight the historical challenges mathematicians faced in understanding negative values and the logical principles that govern multiplication. By defining multiplication through its behavior across different contexts—such as counting numbers, fractions, and geometry—they emphasize the flexibility and universality of mathematical concepts. The speaker ultimately presents mathematics as a beautiful, structured system, encouraging viewers to appreciate its inherent logic and patterns beyond mere practical applications.
Takeaways
- 😀 Understanding multiplication requires recognizing its behavior across different mathematical contexts.
- 🤔 The historical struggle with negative numbers highlights the evolution of mathematical understanding, particularly in the 1800s.
- 🔍 Extending the rules of counting numbers to negative numbers can yield consistent mathematical systems.
- 🧮 Multiplication involving negative numbers, such as -2 times -3, can be logically derived to equal positive values.
- 📐 Multiplication in geometry relates to area, where the order of multiplication (e.g., 4x3 vs. 3x4) does not affect the outcome.
- 🔗 Fractions illustrate how multiplication behaves, with phrases like 'a half of a third' demonstrating practical applications.
- 🎯 The concept of multiplication is defined not by what it is but by how it behaves in various contexts, such as repeated addition and scaling.
- ✨ Mathematics is a beautiful structure that transcends practical applications, deserving appreciation for its own sake.
- 💡 Recognizing the underlying principles of mathematics helps clarify complex concepts and operations.
- 🚀 The discussion emphasizes that there are no absolute definitions in mathematics; instead, context shapes meaning.
Q & A
What is the main topic discussed in the video?
-The main topic discussed is the concept of multiplication, particularly its extension to negative numbers, and the underlying mathematical principles that govern its application.
How does the speaker relate multiplication to counting numbers?
-The speaker explains that multiplication is often understood as repeated addition in the context of counting numbers, and seeks to extend this intuitive understanding to negative numbers.
What historical context is provided regarding the understanding of negative numbers?
-The speaker mentions that negative numbers were a source of struggle in mathematics throughout history, with significant advancements in understanding occurring only in the 1800s when mathematicians began to formalize rules for negative multiplication.
What logical consequence of multiplication involving negative numbers is discussed?
-A key logical consequence discussed is that multiplying two negative numbers results in a positive number, which is counterintuitive but follows from the established rules of arithmetic.
How does the speaker define multiplication in broader terms?
-Multiplication is defined as any operation that behaves according to certain rules, rather than being tied to a specific practical application or context. This includes interpretations in different mathematical domains.
What example does the speaker use to illustrate multiplication with fractions?
-The speaker uses the example of 'a half of a third' to show that multiplication behaves consistently across fractions, comparing it to 'a third of a half' to demonstrate equivalent areas.
How is multiplication connected to geometry in the discussion?
-Multiplication is connected to geometry through the concept of area, where the area of a rectangle is found by multiplying its length by its width, illustrating the same multiplicative principles.
What emphasis does the speaker place on the abstract nature of mathematics?
-The speaker emphasizes that mathematics is an abstract discipline with universal structures that manifest differently depending on the context, highlighting the beauty and complexity of mathematical relationships.
What does the speaker suggest is necessary for understanding mathematical concepts?
-The speaker suggests that recognizing the underlying structures and rules of mathematics is essential for understanding, encouraging a deep exploration of how these concepts interact across various contexts.
How does the speaker view the relationship between practical applications and abstract mathematics?
-The speaker believes that while practical applications of mathematics are important, the true beauty of math lies in its abstract nature and the ability to apply mathematical principles across different scenarios without losing the core structural integrity.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Pengertian Bilangan Rasional

PT3 KSSM Mathematics Form 1 (Rational Numbers) Chapter 1 Complete Revision
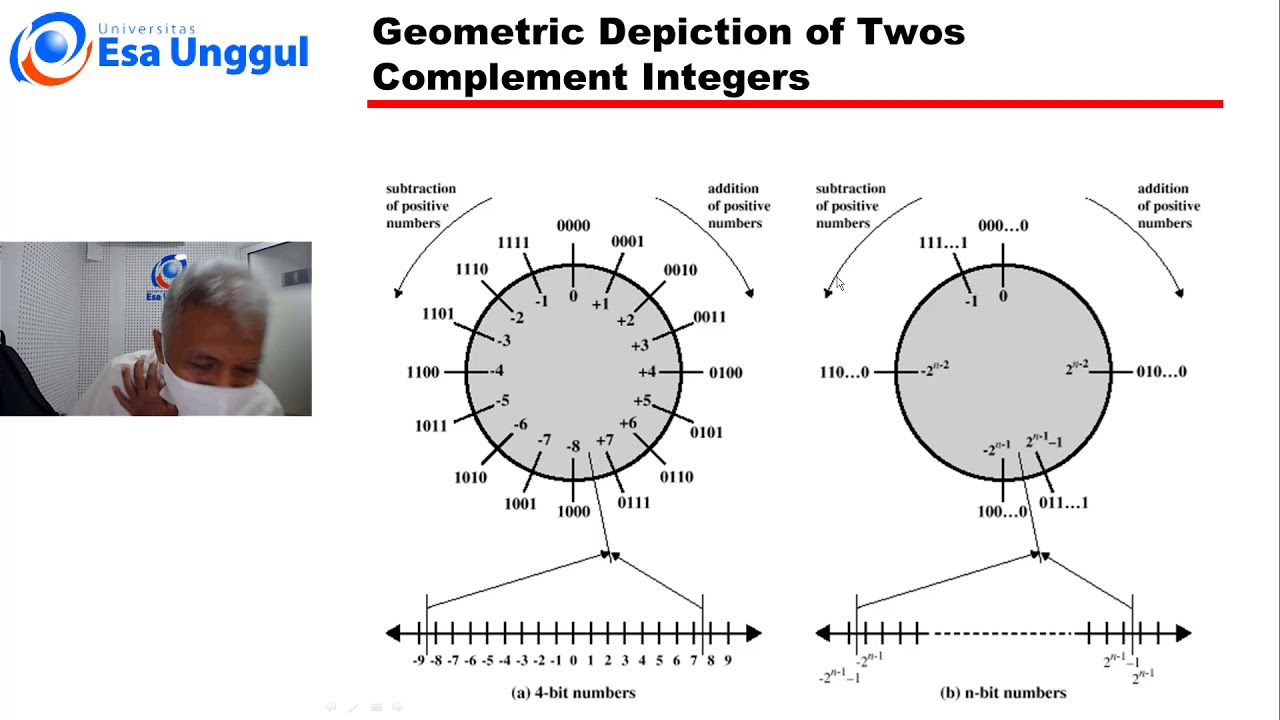
20201 - CCI120 - ORGANISASI DAN ARSITEKTUR KOMPUTER - 10 (BUDI TJAHJONO) ***

How to Multiply and Divide Fractions #10

02.3. Sifat Sifat Penting Bilangan Riil Bagian 2

MATEMATIKA DASAR ke -3 untuk SD, SMP, SMA
5.0 / 5 (0 votes)
