Aproximar un límite con una tabla | Khan Academy en Español
Summary
TLDRIn this video, the concept of finding the limit of a mathematical expression as x approaches 3 is explored. The video starts by demonstrating that the expression is undefined at x = 3 due to a 0/0 indeterminate form. To understand the limit, the presenter uses two tables: one for values approaching 3 from the left and the other from the right. Through evaluating these values, the limit is estimated to approach 1.8. The video aims to provide an intuitive understanding of limits using tables and prepares viewers for more exact methods in future lessons.
Takeaways
- 😀 The goal of the video is to understand the limit of a given expression as x approaches 3.
- 😀 The expression in question is: (x^3 - 3x^2) / (5x - 15).
- 😀 At x = 3, the expression yields 0/0, which is an indeterminate form, meaning it's not defined at that point.
- 😀 To understand the limit, the video uses two tables: one for approaching 3 from the left and one from the right.
- 😀 The left-hand limit refers to approaching 3 with values smaller than 3 (e.g., 2.9, 2.99, 2.999).
- 😀 The right-hand limit refers to approaching 3 with values greater than 3 (e.g., 3.1, 3.01, 3.001).
- 😀 Both the left-hand and right-hand limits are needed to ensure the limit is the same from both directions.
- 😀 The approximate value of the limit from both sides is observed to be 1.8.
- 😀 Using values closer and closer to 3 from both sides gives a more accurate approximation of the limit.
- 😀 The video emphasizes that the limit can be calculated more precisely in the future with the right tools, but for now, a table approach helps build understanding.
Q & A
What is the goal of the video?
-The goal of the video is to help understand the meaning of a limit by analyzing the behavior of an expression as x approaches 3.
Why is the expression not defined at x = 3?
-The expression is not defined at x = 3 because when x is substituted into the expression, both the numerator and the denominator equal zero, resulting in a 0/0 indeterminate form.
How is the behavior of the expression analyzed near x = 3?
-The behavior of the expression near x = 3 is analyzed by constructing tables of values for x approaching 3 from both the left and the right, allowing for an estimation of the limit.
What is the concept of the limit from the left?
-The limit from the left refers to evaluating the expression using values of x that are smaller than 3, i.e., approaching 3 from values less than 3.
What is the concept of the limit from the right?
-The limit from the right refers to evaluating the expression using values of x that are greater than 3, i.e., approaching 3 from values greater than 3.
Why are two tables used in the video instead of just one?
-Two tables are used to make the process more intuitive, one for approaching 3 from the left and one for approaching from the right. However, one table could also be used.
What values are used to approximate the limit from the left?
-To approximate the limit from the left, values like 2.9, 2.99, and 2.999 are used, progressively getting closer to 3 from below.
What values are used to approximate the limit from the right?
-To approximate the limit from the right, values like 3.1, 3.01, and 3.001 are used, progressively getting closer to 3 from above.
How does the limit value change as x gets closer to 3?
-As x gets closer to 3, the values of the expression approach 1.8, indicating that the limit of the expression as x tends to 3 is approximately 1.8.
What does the video suggest about approaching the limit from both sides?
-The video emphasizes that for the limit to exist, the expression must approach the same value from both the left and the right. The approximation of the limit from both sides should yield the same value.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Jika lim x->-3 (x^2+4x+3)/(x+3)=a-1,nilai a adalah...
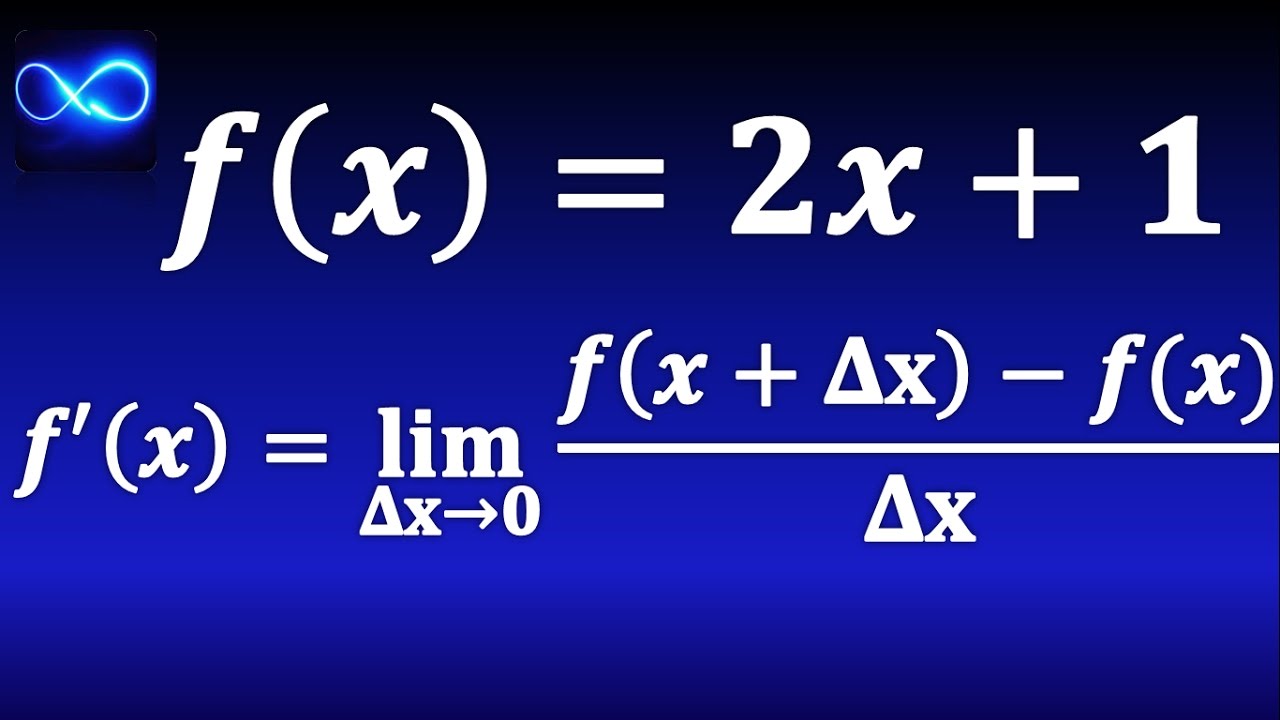
Derivative by increment method (By definition with limit)

Calculating slope of tangent line using derivative definition | Differential Calculus | Khan Academy

Pengertian Limit
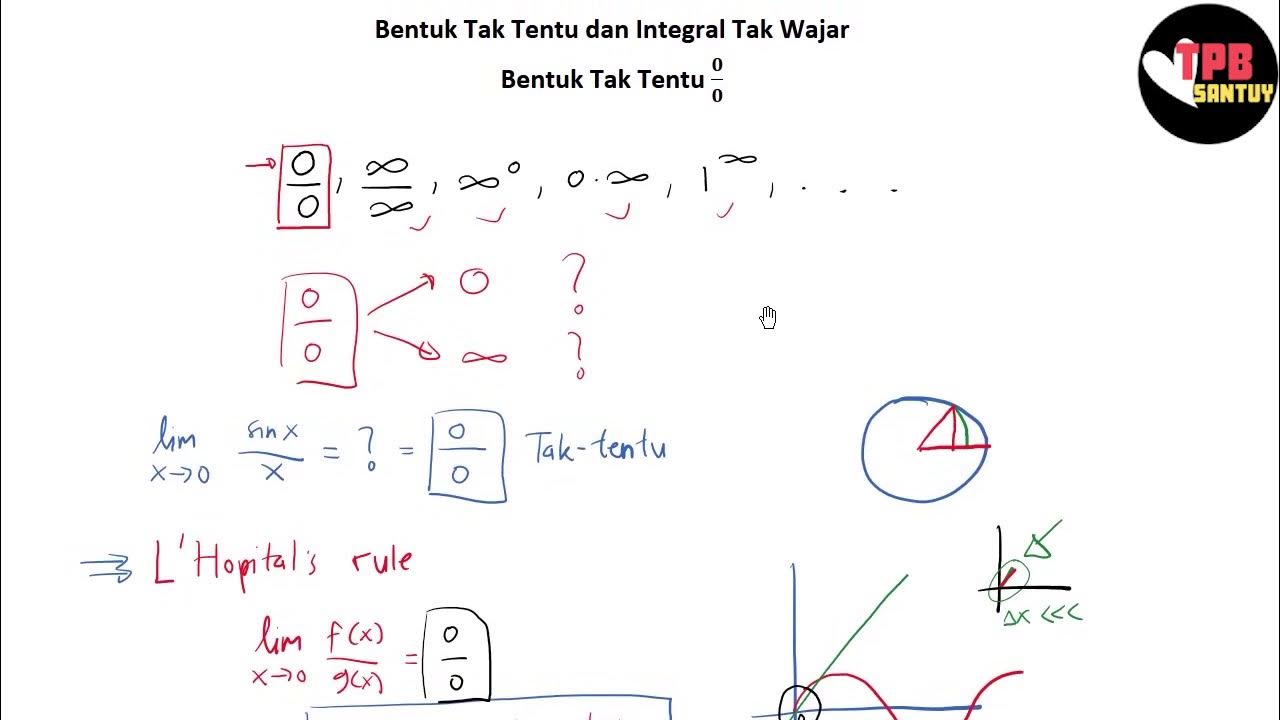
Bentuk 0/0 | Bentuk Tak Tentu dan Integral Tak Wajar (Part 1) | Kalkulus

Limite de una función real de variable real
5.0 / 5 (0 votes)
