PELUANG - Kejadian saling lepas dan tidak saling lepas
Summary
TLDRIn this educational video, the host explains the concept of probability, focusing on mutually exclusive and non-mutually exclusive events. It begins with definitions and formulas, followed by practical examples involving marbles and dice to illustrate the calculations. Viewers learn how to determine probabilities using various scenarios, including the odds of drawing specific colored marbles and rolling dice to achieve certain sums. The video emphasizes the differences between the two types of events and provides clear steps for solving probability problems, making it an informative resource for anyone looking to grasp the fundamentals of probability.
Takeaways
- 📚 The video discusses probability, focusing on disjoint and non-disjoint events.
- 🔍 Disjoint events are defined as events that cannot occur simultaneously.
- 📈 The formula for disjoint events is P(A or B) = P(A) + P(B).
- 🔗 Non-disjoint events can occur at the same time, and their formula is P(A or B) = P(A) + P(B) - P(A and B).
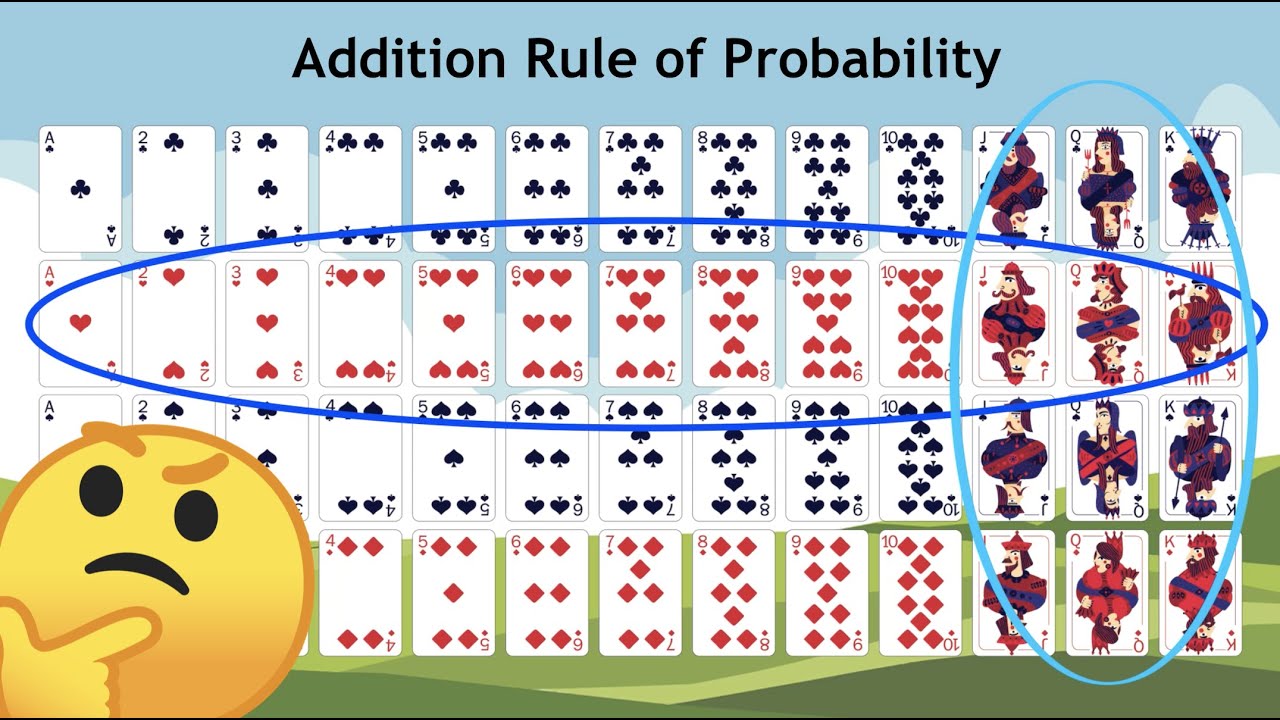
- 🗺️ Venn diagrams are used to visually explain the differences between disjoint and non-disjoint events.
- 🎲 An example of disjoint events involves drawing marbles: if there are 6 red and 4 blue marbles, the chance of drawing a red or blue marble is 1.
- 🎲 Another example involves rolling two dice, calculating the probability of the sum being 4 or 7.
- 📊 The total number of outcomes when rolling two dice is 36.
- 🃏 For non-disjoint events, an example involves drawing numbered cards and calculating the probability of drawing an odd or prime number.
- 🔄 The final answers can often be simplified, demonstrating how to reduce fractions for clarity.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is probability, specifically focusing on mutually exclusive events and non-mutually exclusive events.
What is the definition of mutually exclusive events?
-Mutually exclusive events are defined as two events that cannot occur simultaneously.
What formula is used to calculate the probability of mutually exclusive events?
-The formula used is P(A or B) = P(A) + P(B), where P(A) is the probability of event A, and P(B) is the probability of event B.
How are non-mutually exclusive events defined?
-Non-mutually exclusive events are defined as two events that can occur simultaneously.
What is the formula for calculating the probability of non-mutually exclusive events?
-The formula used is P(A or B) = P(A) + P(B) - P(A and B), where P(A and B) is the probability of both events occurring together.
Can you give an example of mutually exclusive events from the video?
-An example of mutually exclusive events from the video is the event of drawing a red marble or a blue marble from a box, where the two events cannot happen at the same time.
What was the total number of marbles mentioned in the first example?
-The total number of marbles mentioned was 10, consisting of 6 red marbles and 4 blue marbles.
What is the probability of drawing either a red or a blue marble?
-The probability of drawing either a red or a blue marble is 1, meaning it is certain that one of them will be drawn.
What is an example of non-mutually exclusive events given in the video?
-An example of non-mutually exclusive events given in the video is drawing a card that is either odd-numbered or prime-numbered from a set of cards numbered 1 to 10.
What was the conclusion about the probabilities calculated in the examples?
-The conclusion was that for mutually exclusive events, the probability can be directly added, while for non-mutually exclusive events, the intersection must be subtracted to avoid double counting.
What is the final simplified answer for the probability of drawing an odd-numbered or prime-numbered card?
-The final simplified answer for the probability of drawing an odd-numbered or prime-numbered card is 3/5.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

PELUANG KEJADIAN SALING LEPAS DAN TIDAK SALING LEPAS

Peluang (Part 2) | Kejadian Majemuk | Saling Lepas, Tidak Saling Lepas, Saling Bebas, dan Bersyarat

Peluang Kejadian Majemuk (Peluang Saling Lepas dan Tidak Saling Lepas)

PROBABILITY OF UNION OF TWO EVENTS || GRADE 10 MATHEMATICS Q3
Addition Rule of Probability - Explained
"Mutually Exclusive" and "Independent" Events (...are VERY different things!)
5.0 / 5 (0 votes)
