Equilibrium of a particle - Triangle of forces | ExamSolutions
Summary
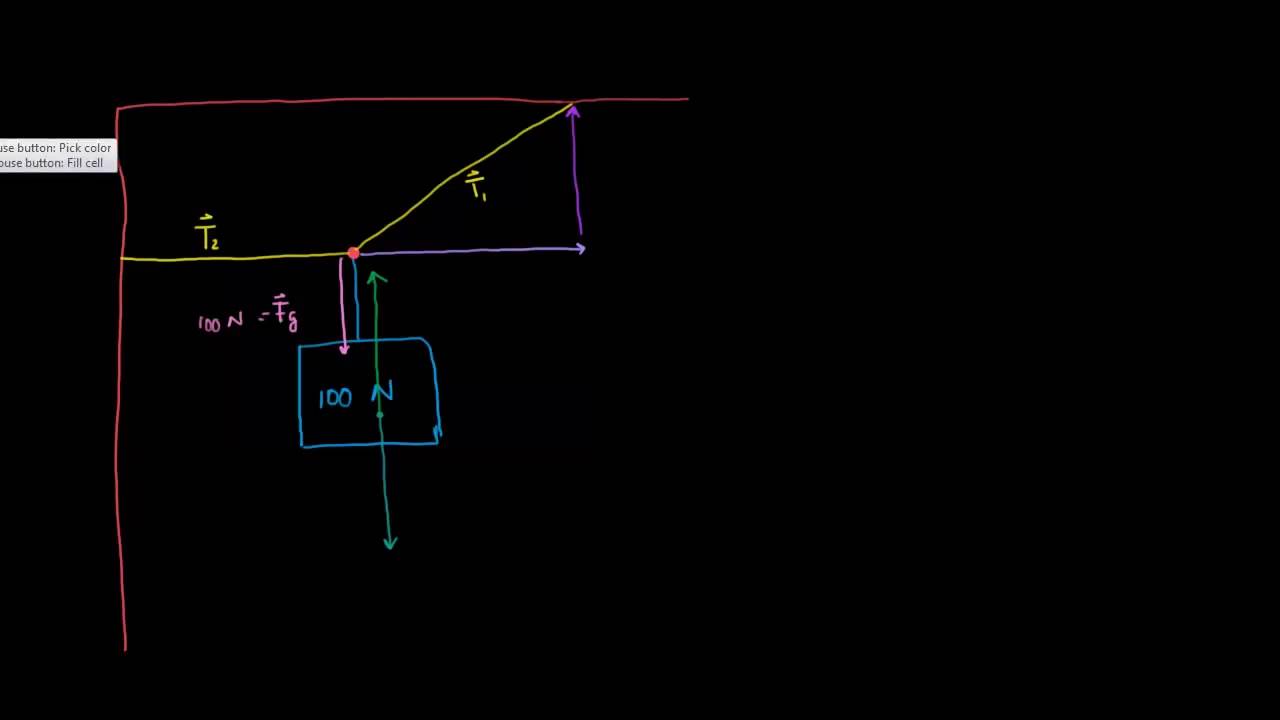
TLDRThis educational script explains how to maintain a particle in equilibrium under the influence of multiple forces. It introduces two methods: the force triangle and resolving forces into components. The force triangle uses the cosine rule to find the resultant force and angle, while resolving involves breaking down forces into horizontal and vertical components to solve for unknown forces and angles. The tutorial uses an example with forces of 8 Newtons and 6 Newtons at a 65° angle to demonstrate these concepts.
Takeaways
- 🔍 The script discusses a physics problem involving forces acting on a particle.
- 📏 It explains how to maintain equilibrium by applying equal and opposite forces.
- 📐 The script introduces a scenario with a force of 6 Newtons at 65° to an 8 Newton force.
- 🔄 It discusses the concept of resultant force and how to calculate it.
- 📈 The script presents two methods for solving the problem: using a force triangle and resolving forces.
- 📖 The force triangle method involves drawing a triangle with the forces and using the cosine rule.
- 📐 The resolving method involves breaking down forces into horizontal and vertical components and setting up equations.
- 🧮 The script provides a step-by-step calculation using both methods, including using trigonometric identities.
- 📉 It explains how to find the unknown force 'P' and angle 'Theta' using the cosine rule and trigonometric functions.
- 🔢 The script concludes with the values of P (11.9 Newtons) and Theta (27°) after calculations.
- 📘 It highlights the preference for the resolving method for problems with more than three forces.
Q & A
What is required to keep a particle in equilibrium if an 8 Newton force acts on it?
-To keep the particle in equilibrium, an equal and opposite force of 8 Newtons must be applied to the particle.
What happens when a 6 Newton force is applied at an angle of 65° to an 8 Newton force?
-The particle will experience a resultant force that acts somewhere between the directions of the 8 Newton and 6 Newton forces. To maintain equilibrium, a force must be applied in the opposite direction of the resultant force.
How can we calculate the force P and angle θ required for equilibrium in this scenario?
-There are two methods to calculate the force P and angle θ: by using a force triangle or by resolving forces into perpendicular directions. Both methods provide the same results.
How is the cosine rule used to calculate the force P?
-Using the cosine rule, P² = 8² + 6² - 2 * 8 * 6 * cos(115°). Solving this equation gives P ≈ 11.9 Newtons.
How do you determine the angle θ using the sine rule?
-By applying the sine rule: sin(θ) / 6 = sin(115°) / P. Solving this gives θ ≈ 27°.
What does the force triangle method help visualize in this situation?
-The force triangle method helps visualize the relationship between the three forces acting on the particle, showing how they form a closed triangle when the particle is in equilibrium.
What is the role of resolving forces horizontally in this problem?
-Resolving forces horizontally allows you to break down the forces acting on the particle into horizontal components. For equilibrium, the sum of all horizontal forces must be zero.
What are the horizontal components of the forces acting on the particle?
-The horizontal components are P cos(θ) to the left, -8 Newtons from the 8 Newton force, and -6 cos(65°) from the 6 Newton force. These components must sum to zero for equilibrium.
Why is resolving forces vertically also necessary in this problem?
-Resolving vertically ensures that the sum of the vertical forces is zero, which is required for equilibrium. The vertical components of the forces must balance each other out.
What is the key identity used to solve for θ and P using the resolving method?
-The key identity is tan(θ) = sin(θ) / cos(θ), which is derived by dividing the vertical force equation by the horizontal force equation. This identity helps solve for θ, and then P can be determined by substitution.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
5.0 / 5 (0 votes)