Cuartiles introducción | Qué son y como encontrarlos en datos sin agrupar
Summary
TLDREn este video, el instructor introduce el concepto de cuartiles en estadística, explicando cómo dividen un conjunto de datos en cuatro partes iguales. A través de ejemplos prácticos, se muestra cómo calcular los cuartiles sin necesidad de fórmulas complicadas, usando una aproximación lógica. Además, se abordan situaciones con números de datos impares y pares, detallando cómo hallar la mediana y los cuartiles 1, 2 y 3, y cómo estos valores representan los percentiles 25%, 50% y 75%. El objetivo es proporcionar una comprensión clara de las medidas de posición en los datos y cómo se aplican en situaciones reales.
Takeaways
- 😀 Los cuartiles son tres valores que dividen un conjunto de datos ordenados en cuatro partes iguales.
- 😀 El cuartil 2 es igual a la mediana, que representa el 50% de los datos.
- 😀 Existen diferentes métodos para calcular los cuartiles, pero se puede hacer tanto con fórmulas como de manera lógica.
- 😀 En un conjunto de datos impar, el cuartil 2 (mediana) es el valor central de los datos ordenados.
- 😀 Cuando el número de datos es par, se obtiene el cuartil 2 promediando los dos valores centrales.
- 😀 Los cuartiles representan los valores del 25%, 50% y 75% de los datos, también conocidos como Q1, Q2 y Q3.
- 😀 El cuartil 1 (Q1) es el valor que divide el 25% inferior de los datos, mientras que el cuartil 3 (Q3) divide el 75% inferior.
- 😀 Los cuartiles se utilizan para interpretar y sacar conclusiones sobre los datos, como los rangos y la dispersión.
- 😀 Si el número de datos es impar, el cálculo del cuartil es directo, mientras que en un número par, el cuartil se obtiene promediando los valores centrales.
- 😀 A la hora de calcular los cuartiles, es importante recordar que los datos deben estar siempre ordenados de menor a mayor antes de hacer cualquier cálculo.
Q & A
¿Qué son los cuartiles en estadística?
-Los cuartiles son tres valores que dividen un conjunto de datos ordenados en cuatro partes iguales. Representan el 25%, 50% y 75% de los datos.
¿Cuál es la relación entre la mediana y el cuartil 2?
-La mediana es el mismo valor que el cuartil 2. El cuartil 2 divide los datos en dos partes iguales, representando el 50% de los datos.
¿Qué pasa si el número de datos es impar al calcular la mediana?
-Cuando el número de datos es impar, la mediana es el valor central de los datos ordenados. Este valor divide los datos en dos mitades iguales.
¿Cómo se calcula la mediana si el número de datos es par?
-Si hay un número par de datos, la mediana se obtiene calculando el promedio de los dos valores centrales, ya que no hay un solo valor en el centro.
En el ejemplo de edades, ¿cómo se calculó el cuartil 2 (mediana) cuando hay 11 datos?
-Con 11 datos, el cuartil 2 es el valor central, que en este caso es el valor en la posición 6, que es 16, ya que a su izquierda y derecha hay igual número de datos.
¿Cómo se determinan los cuartiles 1 y 3 en un conjunto de 11 datos?
-Para encontrar el cuartil 1 y el cuartil 3, se analizan los datos a la izquierda y a la derecha de la mediana (cuartil 2). En cada uno de estos subconjuntos, se selecciona el valor central para obtener los cuartiles.
¿Cómo se calcula la posición de un cuartil utilizando la fórmula?
-La fórmula para calcular la posición de un cuartil es: Posición = (k * (n + 1)) / 4, donde 'k' es el número del cuartil que se busca (1, 2, o 3) y 'n' es el número total de datos.
En un conjunto de 10 datos, ¿cómo se encuentra el cuartil 2?
-Con 10 datos, como hay dos valores centrales, el cuartil 2 se calcula tomando el promedio de estos dos valores. Esto divide el conjunto de datos en dos partes iguales.
¿Qué sucede si el número de datos es par al calcular los cuartiles?
-Si el número de datos es par, para los cuartiles 1 y 3, se deben dividir los datos a la izquierda y derecha de la mediana, calculando los valores centrales de esos subconjuntos.
¿Por qué la lógica es preferida sobre la fórmula al calcular cuartiles en este caso?
-La lógica es preferida en este caso porque permite una comprensión directa de cómo los cuartiles dividen los datos en partes iguales, mientras que la fórmula puede resultar más compleja y menos intuitiva.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Cuartiles, deciles y percentiles Definición e interpretaciones

¿Cómo calcular MEDIDAS DE POSICIÓN en EXCEL? | EXPLICADO

CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
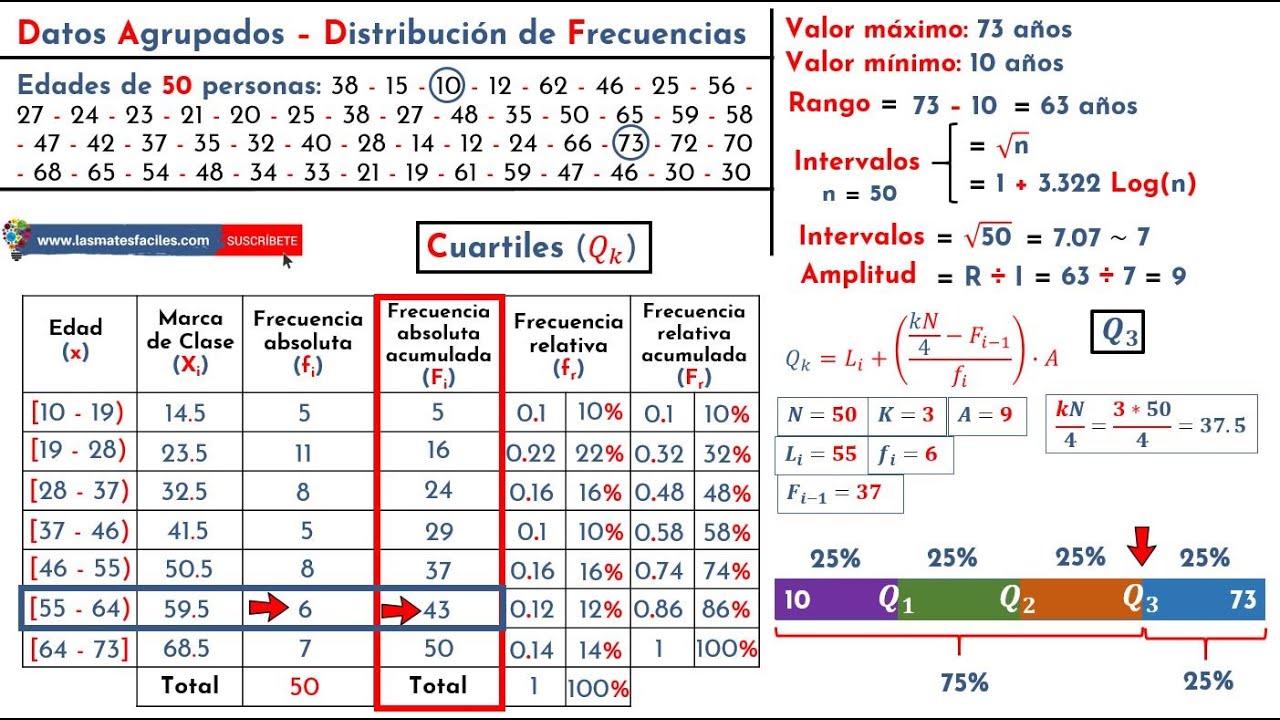
Cuartiles, Deciles y Percentiles - Datos Agrupados
5.0 / 5 (0 votes)
