FUNCIÓN CONTINUA y DISCONTINUA (ejercicio tipo examen)
Summary
TLDREste video educativo aborda la continuidad de funciones, especialmente funciones racionales. Se explica que la discontinuidad ocurre cuando el denominador es cero, lo que impide calcular el valor de la función. Se analizan varios valores de 'x' para determinar la continuidad, identificando que tres valores causan discontinuidad y uno, cuando 'x' tiende a más 1, resulta en una función continua. Se ilustra el proceso de evaluación mediante límites y se demuestra que el límite de la función cuando 'x' tiende a más 1 es -5/3. El video invita a los espectadores a participar en la discusión y a seguir el canal en varias redes sociales.
Takeaways
- 📉 La función es racional, es decir, tiene forma fraccionaria.
- ❌ La función es discontinua cuando el denominador es igual a 0.
- 🔍 El problema se reduce a analizar valores para evitar que el denominador sea cero.
- ✖️ Tres de los valores dados generan discontinuidades, pero uno permite la continuidad.
- 📏 Para analizar continuidad o discontinuidad, se debe evaluar el límite de la función.
- 🧮 Al sustituir x = -2, el denominador se convierte en 0, lo que genera discontinuidad.
- 🟢 Al evaluar x = 1, el límite de la función es -5/3, lo que indica continuidad.
- 🚫 Al sustituir x = 0, el denominador también tiende a 0, lo que genera discontinuidad.
- ➕ Sustituyendo x = 2, se obtiene un denominador distinto de 0, lo que también produce discontinuidad.
- 🎯 La respuesta correcta es el inciso C, ya que es el único valor que genera continuidad en la función.
Q & A
¿Qué tipo de función se discute en el guion del video?
-Se discute una función del tipo racional o con forma fraccionaria.
¿Cuál es la condición para que una función racional sea discontinua?
-Una función racional es discontinua si el denominador es cero, ya que no se puede dividir por cero.
¿Cuál es la estrategia para determinar si un valor de x hace que la función sea continua?
-Analizar si al sustituir el valor de x en el denominador se obtiene cero o no.
¿Qué valor de x hace que la función sea discontinua según el guion?
-Los valores de x que hacen que el denominador sea cero hacen que la función sea discontinua.
¿Cómo se determina si la función es continua para x tending a -2?
-Al analizar si el denominador se anula cuando x tiende a -2.
¿Qué pasa con la función cuando x tiende a 0?
-La función tiende a ser discontinua porque el denominador se anula.
¿Cuál es el resultado del límite de la función cuando x tiende a 1?
-El límite de la función cuando x tiende a 1 es -5/3, lo que indica que la función es continua en ese punto.
¿Por qué la función no es continua cuando x tiende a 2 según el guion?
-La función no es continua cuando x tiende a 2 porque el denominador se anula, lo que causa una discontinuidad.
¿Cuál es el inciso que indica la continuidad de la función en el guion?
-El inciso c indica que la función es continua cuando x tiende a 1.
¿Cuáles son las redes sociales mencionadas en el guion para seguir más contenido del canal?
-Facebook, Instagram, Twitter y TikTok.
¿Qué se sugiere hacer si el espectador quiere más contenido similar?
-Se sugiere dejar un comentario y suscribirse al canal.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
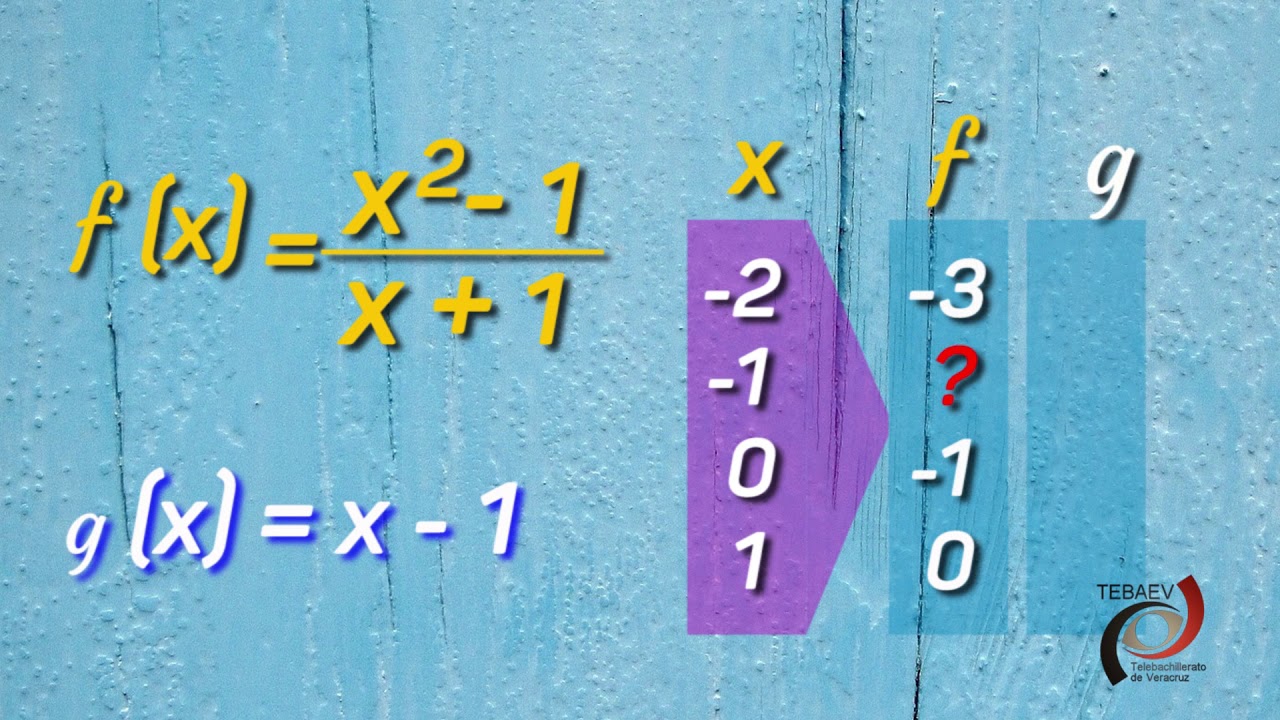
Concepto e interpretación de límites.

►¿Cómo Calcular Límites y Continuidades de la Gráfica de una Función?

👉 CONTINUIDAD de una función Concepto Ejemplos 🔝 Tipos de discontinuidad

Función Racional - Ejercicios Nivel 1 - Introducción

Pensamiento matemático 3. Progresión 2b. Funciones y tipos de funciones

Hallar el DOMINIO de una FUNCIÓN 📉 Funciones
5.0 / 5 (0 votes)
