Solution to Moon Problem 211
Summary
TLDRIn the video, Keith Norman discusses a problem involving launching a satellite into a circular orbit around the Moon. He explains the necessary calculations for achieving a stable orbit, including determining the circular velocity (1.68 km/s) and period (1.8 hours). Keith also covers the concept of escape velocity, which is 2.38 km/s, and how it relates to the formation of elliptical and hyperbolic orbits. The video provides a clear understanding of orbital mechanics and the factors influencing satellite trajectories.
Takeaways
- 📅 Today's date is Monday, September 16, 2024.
- 🎥 The video is a solution by Keith Norman to a problem, not specified as difficult.
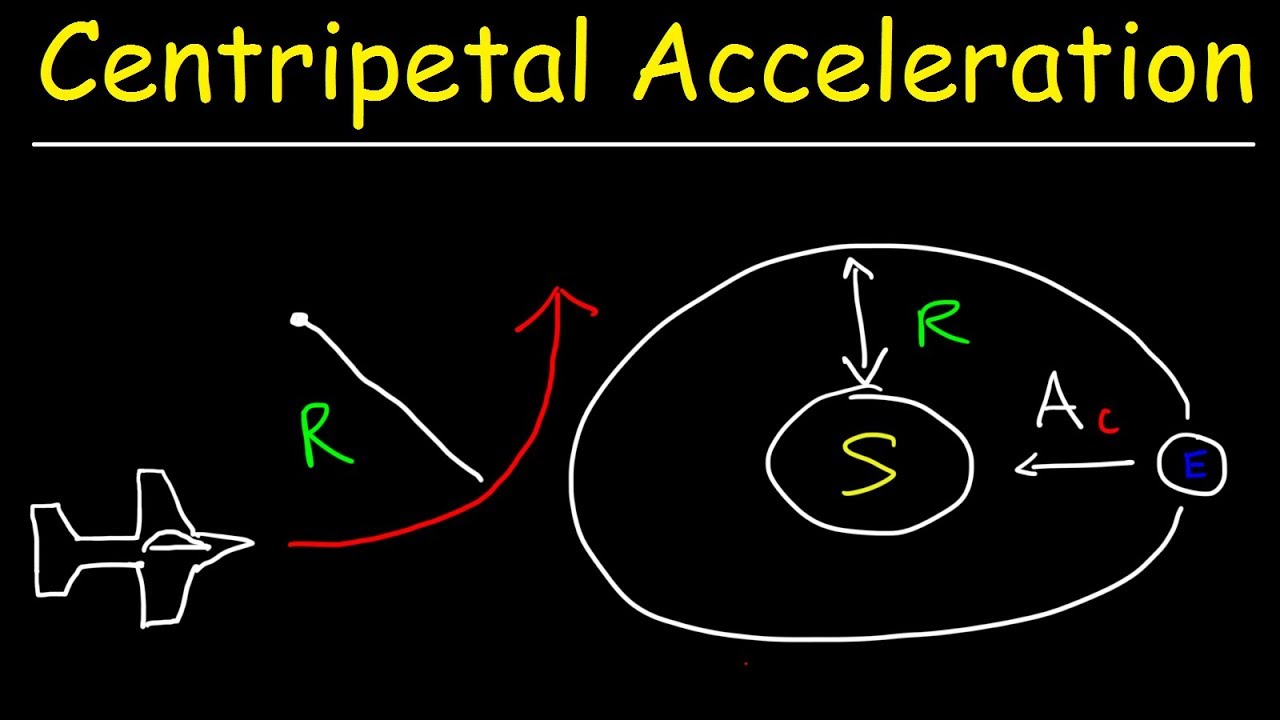
- 🌕 The problem involves launching a satellite into a circular orbit around the Moon.
- 🚀 The satellite is launched from a gun with an adjustable velocity to achieve circular orbit.
- 📐 The gravitational force between the Moon and the satellite must equal the centripetal force for a circular orbit.
- 🔢 For a circular orbit, the calculated velocity is 1.68 km/s, and the period is approximately 1.8 hours or 6,496 seconds.
- 🌐 Part B and Part C of the problem require understanding of escape velocity, derived in lecture 14.
- 💨 The escape velocity, related to the circular velocity by a factor of √2, is calculated to be 2.38 km/s.
- 🛰️ For velocities less than escape velocity, the orbit is bound and elliptical; for velocities above, the orbit is unbound and hyperbolic.
- 📉 As velocity increases beyond the minimum for a stable orbit, the focus of the elliptical orbit moves further away, eventually leading to a parabolic and then hyperbolic path.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the solution to Walter Le's problem 2011 by Keith, which involves calculations related to a satellite's orbit around the Moon.
What is the significance of the number 1.68 km/s mentioned in the script?
-The number 1.68 km/s is the calculated circular velocity required for a satellite to maintain a stable circular orbit around the Moon.
What is the period of the satellite's orbit as described in the script?
-The period of the satellite's orbit is approximately 1.8 hours or 6,496 seconds.
What is the escape velocity from the Moon, as discussed in the script?
-The escape velocity from the Moon is calculated to be 2.38 km/s, which is derived by multiplying the circular velocity by the square root of 2.
What type of orbit does the satellite have if it is launched at a velocity of 2 km/s, according to the script?
-If the satellite is launched at a velocity of 2 km/s, it will have a bound elliptical orbit.
What happens to the satellite's orbit if it is launched at a velocity greater than the escape velocity?
-If the satellite is launched at a velocity greater than the escape velocity, it will have an unbound hyperbolic orbit and will not return to the Moon.
What is the minimum velocity required for a stable orbit around the Moon, as per the script?
-The minimum velocity required for a stable orbit around the Moon is 1.68 km/s.
What is the relationship between the gravitational force and the centripetal force for a satellite in a circular orbit, as explained in the script?
-For a satellite in a circular orbit, the gravitational force between the satellite and the Moon must match the centripetal force required for circular motion.
What is the role of the gravitational constant in calculating the satellite's orbit, according to the script?
-The gravitational constant is used in the calculations to determine the force of gravity between the satellite and the Moon, which is essential for determining the satellite's orbit.
Why does the script mention that being a few meters above the Moon's surface does not significantly affect the calculations?
-The script mentions that being a few meters above the Moon's surface does not significantly affect the calculations because the Moon's radius is approximately 1.7 million meters, making a small height difference negligible.
What is the focus of an elliptical orbit, and how does it relate to the satellite's velocity, as discussed in the script?
-In an elliptical orbit, one focus remains at the center of the Moon, and the other focus moves away as the satellite's velocity increases. At a certain velocity, the second focus moves to infinity, indicating a parabolic path.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)