Circuito de 3 mallas análisis matemático
Summary
TLDREl video muestra cómo obtener el modelado matemático de un circuito con tres mallas formadas por elementos pasivos como resistores, capacitores e inductores. Se detallan los pasos para etiquetar las corrientes y polaridades de cada malla, seguido de la aplicación de la Ley de Voltajes de Kirchhoff para obtener las ecuaciones que describen el sistema. Se realiza el análisis en términos de la carga y se explica cómo las corrientes y voltajes están relacionados. Finalmente, se ofrecen simplificaciones algebraicas para hacer más claro el sistema de ecuaciones resultante.
Takeaways
- 😀 El video trata sobre cómo obtener el modelado matemático de un circuito compuesto por diferentes elementos pasivos que forman tres mallas.
- 🔌 Se describe el etiquetado de las corrientes en cada malla y las polaridades de los elementos según la convención de flujo de corriente horario.
- ⚡ Se aplica la ley de voltajes de Kirchhoff para desarrollar ecuaciones para cada una de las mallas, resultando en tres ecuaciones fundamentales.
- 🔄 Se enfatiza la importancia de la carga como variable fundamental en el modelado, y se relaciona con la corriente a través del operador de derivada.
- 📚 Se recomienda revisar videos pasados para comprender las relaciones lineales entre los diferenciales de potencial y las constantes de los elementos resistor, capacitor e inductor.
- 🔢 Se reescriben las ecuaciones en términos de carga, mostrando cómo los capacitores y los inductores contribuyen al modelo matemático del circuito.
- 📐 Se utiliza álgebra para simplificar y clarificar las ecuaciones, facilitando la visualización y resolución del modelo matemático.
- 🔍 Se destaca la interconexión entre las mallas a través de los capacitores, y cómo esto afecta la dinámica de la corriente en cada malla.
- 📉 Se factorizan términos comunes en las ecuaciones para presentar un sistema de ecuaciones más limpio y organizado.
- 🤔 Se invita a los espectadores a dejar comentarios si tienen dudas, resaltando la intención educativa y colaborativa del video.
Q & A
¿Qué es el modelado matemático de un circuito y cómo se relaciona con los elementos pasivos?
-El modelado matemático de un circuito es el proceso de representar el comportamiento de un circuito eléctrico mediante ecuaciones matemáticas. Se relaciona con los elementos pasivos, como resistores, capacitores e indutores, ya que estos tienen propiedades que se pueden describir mediante relaciones matemáticas, como la ley de Ohm para los resistores y las ecuaciones que relacionan la tensión con la carga y la corriente para capacitores e indutores.
¿Qué es una malla en un circuito y cómo se determina el flujo de corriente en ella?
-Una malla en un circuito es un circuito cerrado formado por elementos resistivos y pasivos. El flujo de corriente en una malla se determina siguiendo la convención de flujo de corriente, que es horario en este caso, y se etiqueta para cada una de las mallas con una corriente específica, como i1, i2, e i3.
¿Cómo se etiquetan las polaridades de los elementos en un circuito para el análisis de mallas?
-Las polaridades de los elementos en un circuito se etiquetan siguiendo el sentido de la corriente. Por ejemplo, si la corriente fluye de un terminal positivo a un terminal negativo, la polaridad se etiqueta como positivo negativo. Esto se hace para cada elemento en cada malla, de acuerdo con la dirección de la corriente.
¿Qué es la ley de voltajes de Kirchhoff y cómo se aplica en el análisis de mallas?
-La ley de voltajes de Kirchhoff establece que la suma de los voltajes alrededor de cualquier circuito cerrado es cero. Se aplica en el análisis de mallas al sumar los voltajes generados por los elementos del circuito en una malla y establecer que la suma de estos voltajes es igual a cero, lo que resulta en una ecuación para cada malla.
¿Cuál es la diferencia entre modelar un circuito en términos de corriente y en términos de carga?
-Modelar un circuito en términos de corriente implica describir el comportamiento del circuito en función de las corrientes que fluyen a través de los elementos. En cambio, modelar en términos de carga implica describir el comportamiento en función de la carga almacenada en los capacitores y su relación con la corriente, ya que la corriente es el cambio de carga con el tiempo.
¿Cómo se relaciona la ecuación diferencial con el modelado matemático de un circuito?
-Las ecuaciones diferenciales son fundamentales en el modelado matemático de un circuito, ya que describen cómo las variables cambian con el tiempo. En el caso de un circuito, estas ecuaciones pueden relacionar la corriente (u su derivada) con la tensión en los elementos como capacitores e indutores.
¿Qué significa 'q1 - q2' en el contexto de un capacitor que une dos mallas?
-En el contexto de un capacitor que une dos mallas, 'q1 - q2' representa la diferencia de carga entre los dos extremos del capacitor. Esto indica la carga relativa que fluye por el capacitor y es clave para entender cómo la carga se distribuye en el circuito.
¿Cómo se aplican las leyes de Ohm y la relación de corriente-derivada en el modelado de un circuito?
-La ley de Ohm se aplica al modelar los resistores, donde la tensión es directamente proporcional a la corriente y la constante de proporcionalidad es la resistencia. La relación de corriente-derivada se aplica a los capacitores e indutores, donde la tensión en un capacitor está relacionada con la tasa de cambio de la carga (primera derivada de la carga) y la tensión en un inductor está relacionada con la tasa de cambio de la corriente (segunda derivada de la carga).
¿Qué es la simplificación algebraica de las ecuaciones en el modelado matemático de un circuito y por qué es útil?
-La simplificación algebraica de las ecuaciones es el proceso de reorganizar y factorizar términos para que las ecuaciones sean más claras y fáciles de entender. Esto es útil porque facilita la identificación de patrones y la resolución de las ecuaciones, lo que a su vez ayuda a comprender mejor el comportamiento del circuito.
¿Cómo se determina la 'excitation' de la corriente en cada malla durante el análisis de un circuito?
-La 'excitation' de la corriente en cada malla se determina por los elementos que suministran un voltaje o una diferencia de potencial que causa el flujo de corriente. Por ejemplo, en una malla, el capacitor que comparte con otra malla puede proporcionar la excitación necesaria para el flujo de corriente, como se ve en la ecuación donde el voltaje del capacitor 1 influye en la malla 2.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Elementos PASIVOS y ACTIVOS de un CIRCUITO ELÉCTRICO ➤ y sus 7 SIMBOLOS 😱 [LO QUE NO TE ENSEÑAN] ⚠️

ACDC 1.1.1 Conceptos generales

Elementos pasivos y activos - electronica fácil!

Circuito Doble Malla

El MEJOR y MÁS SENCILLO "PIANO" con 555 | Tutorial PASO A PASO
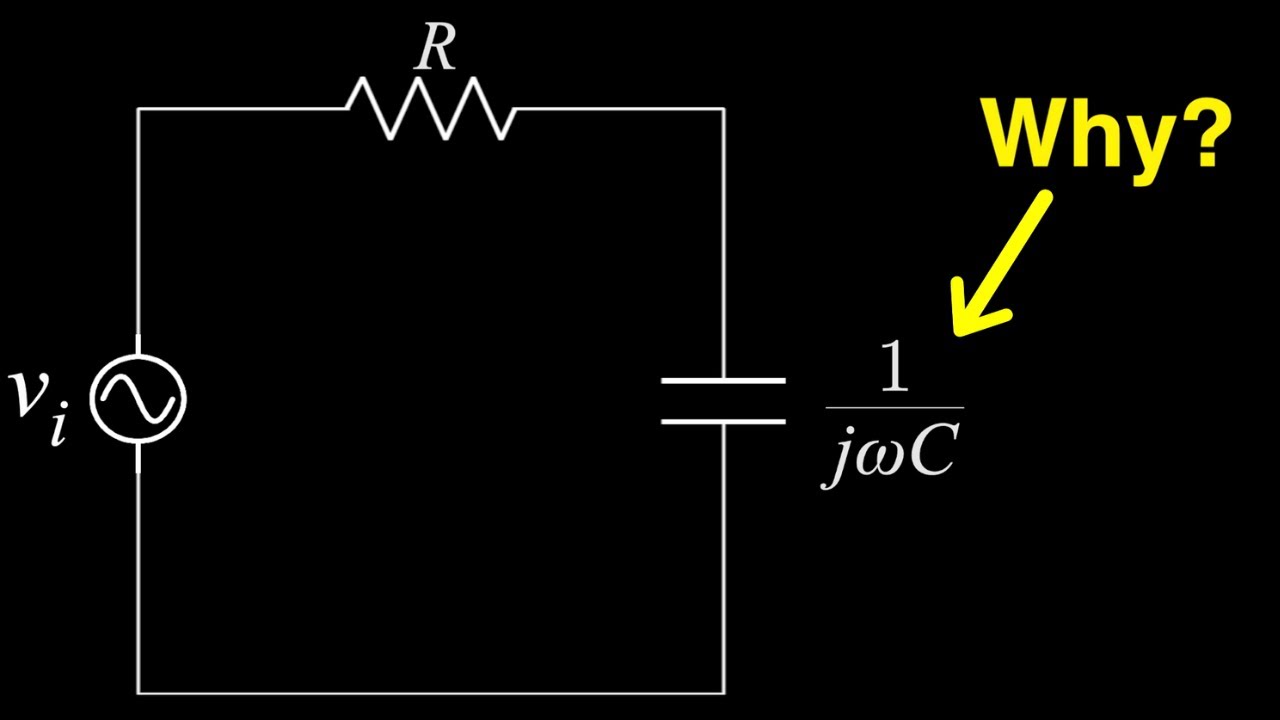
Why do Electrical Engineers use imaginary numbers in circuit analysis?
5.0 / 5 (0 votes)
