Funciones de activación en las redes profundas
Summary
TLDREn este video, se explora el rol crucial de las funciones de activación en las redes neuronales. Se destaca que, aunque las combinaciones lineales son fundamentales en la calculación de la salida de una neurona, el uso exclusivo de estas combinaciones restringiría el modelo a ser lineal. Por ello, las funciones de activación, como la sigmoide y la tangente hiperbólica, son esenciales para introducir no linealidad, permitiendo a la red representar funciones más complejas. Además, se discuten las ventajas y desventajas de estas funciones, incluyendo el problema del desvanecimiento del gradiente. Se presenta la función ReLU (Rectified Linear Unit) como una solución eficiente a este problema, destacando su capacidad para mejorar el entrenamiento de redes neuronales profundas en tareas como la visión computacional. Finalmente, se resalta que la elección de la función de activación depende del problema específico y que lo más recomendable es probar diferentes funciones para encontrar la más adecuada.
Takeaways
- 🧠 La función de activación es necesaria en las redes neuronales para romper la linealidad de los productos punto y permitir la representación de funciones más complejas.
- 📈 La función sigmoide es utilizada en la regresión logística y su dominio de salida es entre 0 y 1, lo que la hace adecuada para problemas de clasificación binaria.
- 📉 La tangente hiperbólica amplía el rango de salida entre -1 y 1, lo que puede ser útil para problemas que requieren un rango más amplio de valores.
- 🔍 El problema del desvanecimiento del gradiente ocurre cuando los gradientes se vuelven muy pequeños a medida que se retropropagan a través de las capas de la red, lo que dificulta el entrenamiento.
- 🚀 La función de activación ReLU (Rectified Linear Unit) tiene propiedades que mitigan el problema del desvanecimiento del gradiente y es especialmente útil en redes con muchas capas.
- ➡️ La elección de la función de activación depende del problema en particular y no hay una regla estricta sobre cuál es la mejor opción; es una decisión empírica.
- 🤖 Las funciones de activación son fundamentales para el funcionamiento de las redes neuronales, ya que definen cómo las neuronas reaccionarán ante diferentes niveles de activación.
- 📊 La gráfica de la función de activación muestra su comportamiento y cómo se desplaza el equilibrio para representar diferentes rangos de salida.
- 🔢 La función sigmoide, aunque útil, tiene la limitación de limitar los valores de salida entre 0 y 1, lo que puede no ser ideal para todos los tipos de problemas.
- 📌 La función ReLU es simple en su definición y se ha popularizado debido a su efectividad en la extracción de características en redes neuronales profundas.
- 🔧 El ajuste de los pesos en las redes neuronales se ve afectado por el gradiente calculado, el cual es influenciado directamente por la elección de la función de activación.
Q & A
¿Por qué son necesarias las funciones de activación en las redes neuronales?
-Las funciones de activación son necesarias porque permiten romper la linealidad de las combinaciones lineales y darle a la red neuronal la capacidad de representar funciones más complejas.
¿Qué sucede si solo se utilizan combinaciones lineales en una red neuronal?
-Si solo se utilizan combinaciones lineales, incluso con múltiples capas, el resultado sigue siendo lineal y se podría representar como una sola capa, lo que limita la capacidad de la red para aprender funciones complejas.
¿Cuál es la función de activación más utilizada en la regresión logística?
-La función de activación más utilizada en la regresión logística es la función sigmoide.
¿Cómo se define la función sigmoide y cuál es su rango de salida?
-La función sigmoide se define como 1 / (1 + e^(-x)) y su rango de salida está entre 0 y 1.
¿Qué función de activación se utiliza cuando se desea un rango de salida más amplio que el sigmoide?
-Cuando se desea un rango de salida más amplio que el sigmoide, se utiliza la función tangente hiperbólica (tanh).
¿Cómo se define la función de activación tangente hiperbólica y cuál es su rango de salida?
-La función de activación tangente hiperbólica se define como (e^(x) - e^(-x)) / (e^(x) + e^(-x)) y su rango de salida está entre -1 y 1.
¿Qué es el problema del desvanecimiento del gradiente y cómo afecta el entrenamiento de una red neuronal?
-El problema del desvanecimiento del gradiente ocurre cuando los gradientes se van haciendo más pequeños a medida que se utiliza el algoritmo de retropropagación, lo que hace que el ajuste de los pesos sea muy lento y dificulte el entrenamiento, especialmente en capas profundas de la red.
¿Cuál es una función de activación que ayuda a mitigar el problema del desvanecimiento del gradiente?
-La función de activación ReLU (Rectified Linear Unit) ayuda a mitigar el problema del desvanecimiento del gradiente al mantener una pendiente constante de 1 para valores positivos.
¿Cómo se define la función de activación ReLU y cuál es su ventaja principal?
-La función de activación ReLU se define como max(0, x). Su ventaja principal es que para valores positivos, mantiene una pendiente de 1, lo que ayuda a evitar el desvanecimiento del gradiente y permite un entrenamiento más rápido.
¿En qué tipo de problemas funciona mejor la función de activación ReLU?
-La función de activación ReLU funciona mejor en problemas de visión computacional y en redes neuronales con muchas capas, como las redes neuronales convolucionales.
¿Cómo se debe seleccionar la función de activación en una red neuronal?
-La selección de la función de activación depende en gran medida de la experiencia empírica y del problema específico que se esté abordando. No existe una regla clara, pero en general, algunas funciones como la sigmoide, la tangente hiperbólica y la ReLU son comunes y han demostrado buen desempeño en diferentes situaciones.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Funciones de Activación de Redes Neuronales: Sigmoide, ReLU, ELU, Tangente hiperbólica, Softplus y ➕

5.9 Aprendizaje profundo

Funciones de activación a detalle (Redes neuronales)

¿Qué es una Red Neuronal? Parte 2 : La Red | DotCSV

Tu primer clasificador de imágenes con Python y Tensorflow
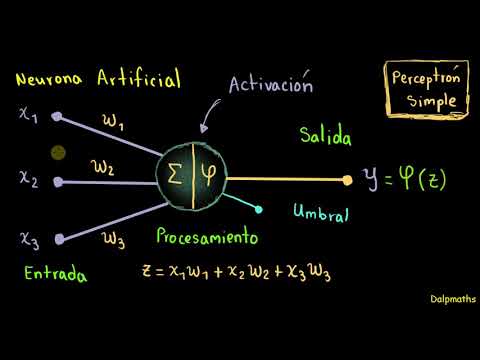
Redes neuronales: Introducción al perceptrón simple.
5.0 / 5 (0 votes)