Velocidad Instantánea
Summary
TLDREl video explica cómo calcular la velocidad instantánea, destacando la diferencia con la velocidad media, ya que esta última no es útil cuando la velocidad varía. Se ilustra con ejemplos, como el caso de un ciclista que recorre una corta distancia en 0.1 segundos, donde se calcula la velocidad instantánea dividiendo la diferencia de distancias por el tiempo. Además, se presenta otro ejemplo usando derivadas para encontrar la velocidad instantánea de un auto en función de su posición respecto al tiempo. Es un recurso claro y útil para aprender sobre este concepto de física.
Takeaways
- 🚴♂️ Si la velocidad no es constante, la velocidad media no es adecuada para determinar la velocidad en un punto específico.
- ⏱️ La velocidad instantánea nos da la velocidad exacta en un momento específico del intervalo.
- 📏 La fórmula de la velocidad instantánea es similar a la de la velocidad media, pero el intervalo de tiempo se hace cada vez más pequeño.
- ⚡ La velocidad instantánea se puede entender como la derivada de la distancia respecto al tiempo.
- 🚴♀️ Ejemplo: Si un ciclista recorre 20 metros en 0.1 segundos, su velocidad instantánea es de 200 metros por segundo.
- 🔢 La velocidad instantánea se puede calcular mediante derivadas, siempre que se tenga la función de posición respecto al tiempo.
- 🚗 Ejemplo: Si un auto tiene una posición de 4t² en un segundo específico, la velocidad instantánea en t=2 segundos es 16 metros por segundo.
- 📉 Para encontrar la velocidad instantánea, se deriva la función de posición respecto al tiempo.
- 🔄 Para obtener la velocidad instantánea en otro instante, se sustituye el tiempo en la variable correspondiente.
- 👍 El video invita a suscribirse y continuar aprendiendo sobre estos temas.
Q & A
¿Qué diferencia hay entre la velocidad media y la velocidad instantánea?
-La velocidad media mide el cambio de posición sobre un intervalo de tiempo más largo, mientras que la velocidad instantánea mide la velocidad en un punto específico o instante del tiempo.
¿Cómo se calcula la velocidad instantánea según el video?
-La velocidad instantánea se calcula dividiendo la diferencia de distancias entre un intervalo de tiempo muy pequeño. En casos más complejos, se utiliza la derivada de la posición con respecto al tiempo.
¿Qué representa la derivada de la función de posición respecto al tiempo?
-La derivada de la función de posición con respecto al tiempo representa la velocidad instantánea en cualquier instante dado.
¿En qué tipo de situaciones sería más útil calcular la velocidad instantánea en lugar de la media?
-La velocidad instantánea es útil cuando la velocidad no es constante, y se quiere conocer la velocidad en un punto o instante específico, como en el caso de un ciclista o un automóvil que cambia su velocidad rápidamente.
¿Qué sucede cuando el intervalo de tiempo se hace cada vez más pequeño en el cálculo de la velocidad?
-Cuando el intervalo de tiempo se hace más pequeño, la velocidad media se aproxima a la velocidad instantánea, ya que se está midiendo la velocidad en un instante cada vez más cercano a cero.
En el ejemplo del ciclista, ¿cómo se calcula la velocidad instantánea?
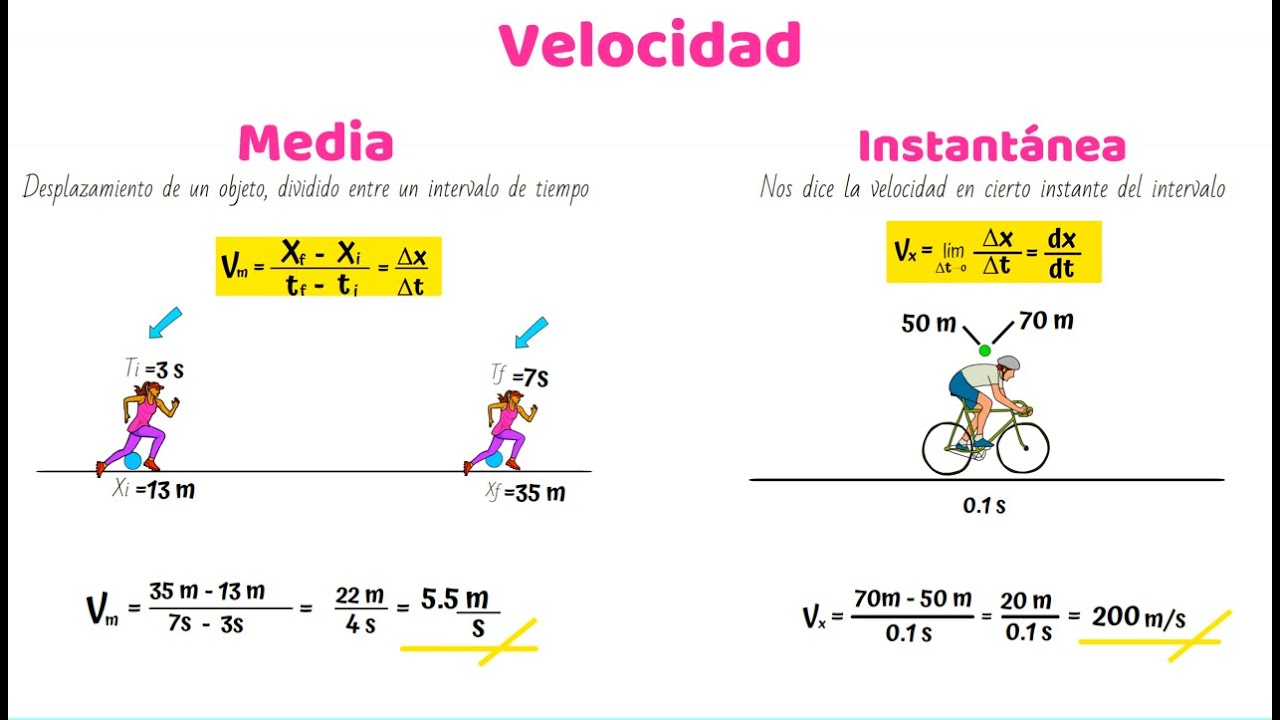
-La velocidad instantánea se calcula restando las distancias recorridas (70 m - 50 m = 20 m) y dividiendo entre el tiempo transcurrido (0.1 segundos), lo que da una velocidad de 200 m/s.
¿Por qué es importante que el intervalo de tiempo sea pequeño para calcular la velocidad instantánea?
-Es importante porque la velocidad instantánea se mide en un instante específico, y un intervalo de tiempo más grande solo proporcionaría una velocidad media, que no refleja cambios rápidos.
En el segundo ejemplo del video, ¿cómo se encuentra la velocidad instantánea del automóvil en el tiempo t = 2 segundos?
-Se deriva la función de posición (4t^2), obteniendo 8t. Luego, se sustituye t = 2 en la función derivada, obteniendo 8 * 2 = 16 m/s.
¿Cómo se relaciona la función de posición con la velocidad en física?
-La función de posición describe la ubicación de un objeto en función del tiempo, y su derivada nos da la velocidad instantánea del objeto en cualquier momento.
¿Qué información adicional se necesita para calcular la velocidad instantánea usando derivadas?
-Se necesita conocer la función de posición del objeto respecto al tiempo. Con esta información, se puede derivar la función para encontrar la velocidad instantánea en un tiempo específico.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

🏎️🏎️VELOCIDAD MEDIA VS INSTANTÁNEA (CONCEPTO Y EJEMPLO)
Velocidad Media e Instantánea

04. Diferencia entre velocidad y rapidez

El concepto de derivada. ¿Qué es y para qué sirve la derivada?

¿CUÁL ES LA DIFERENCIA ENTRE VELOCIDAD MEDIA Y RAPIDEZ MEDIA DE UN MOVIMIENTO? EJEMPLOS EXPLICATIVOS

Velocidad del sonido vs temperatura del ambiente
5.0 / 5 (0 votes)