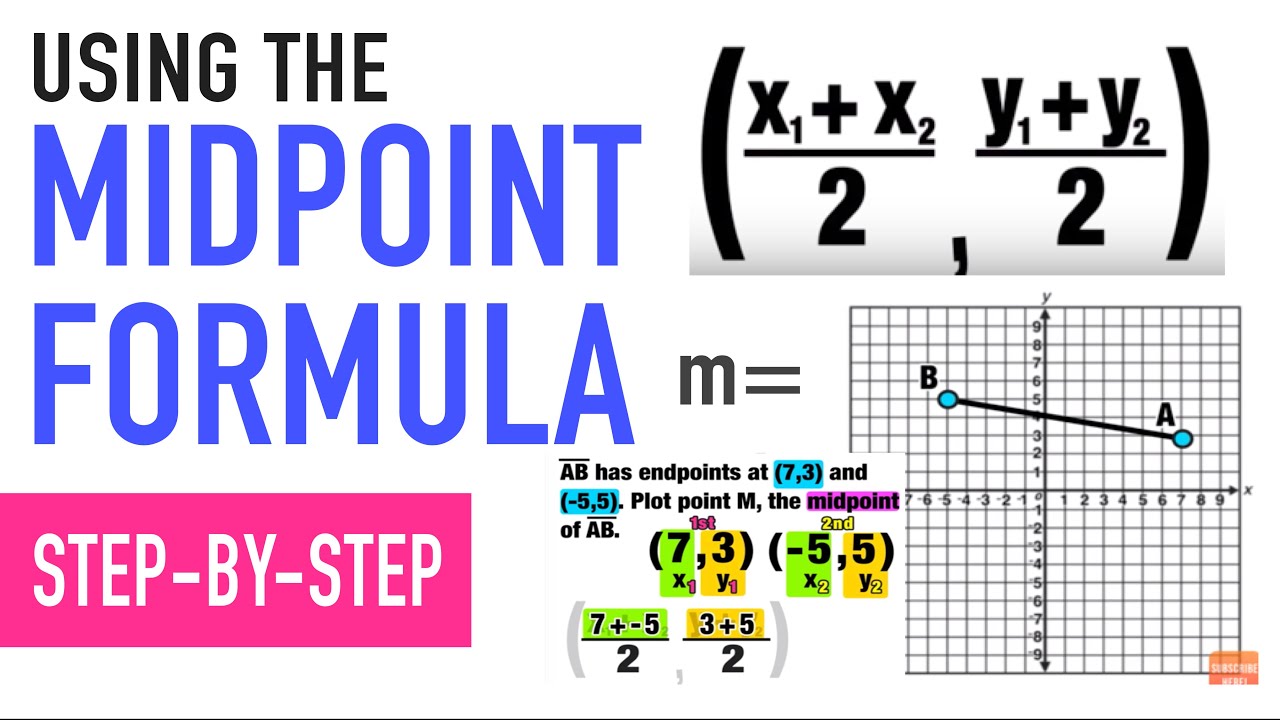
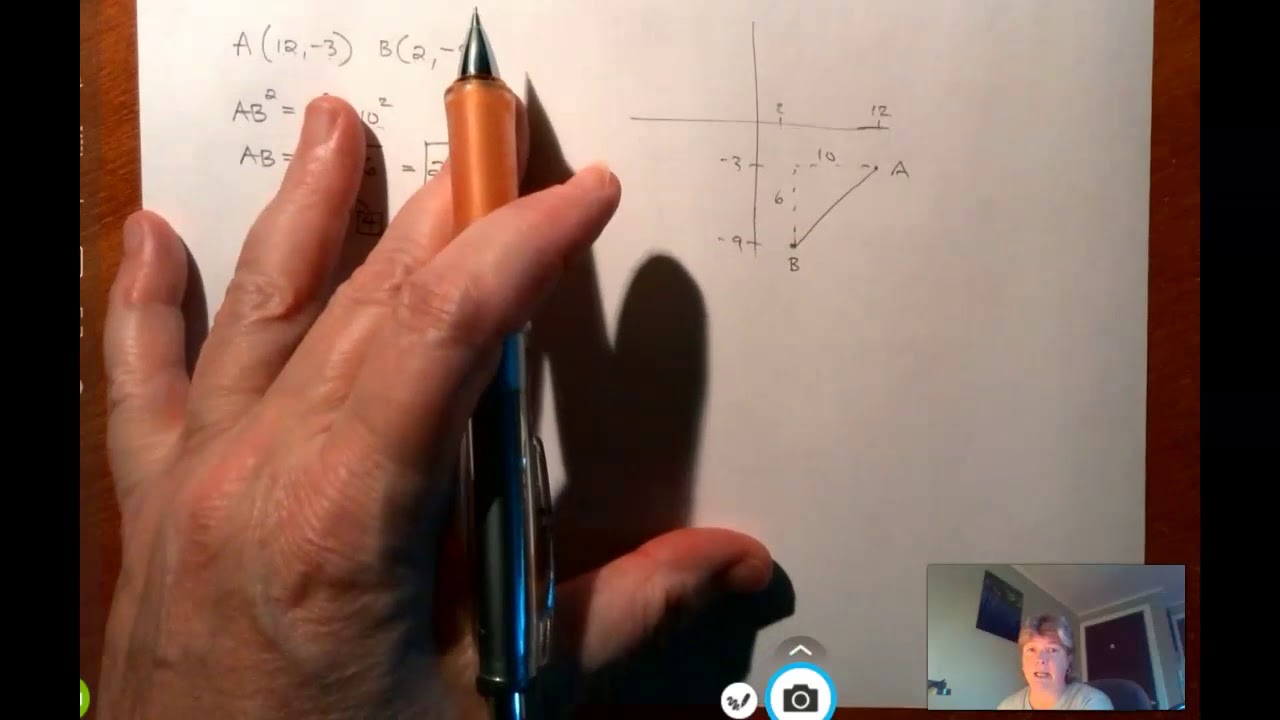
Midpoint of a Line Segment (2nd) Second Quarter Grade 8 Matatag Revised K-12 Tagalog Math Tutorial

Summary

In this educational video, Matt EasyP teaches viewers how to find the midpoint of a line segment on a Cartesian plane, using real-life examples like friends meeting halfway between their houses. The lesson begins with a review of distance calculations and introduces the midpoint formula: M = ((x₁ + x₂)/2, (y₁ + y₂)/2). Step-by-step examples demonstrate midpoints for horizontal, vertical, and diagonal segments, followed by practice problems involving a drone, hikers, and a ship. The video also connects the concept to life lessons, emphasizing fairness, teamwork, and meeting halfway in relationships, making math both practical and relatable.

Takeaways

• 😀 The lesson focuses on finding the midpoint of a line segment on the Cartesian plane.
• 😀 The midpoint formula is M = ((x1 + x2)/2, (y1 + y2)/2).
• 😀 The midpoint divides a line segment into two equal parts.
• 😀 Horizontal, vertical, and diagonal distances between points can be calculated using different methods, including the distance formula.
• 😀 Worked examples demonstrate how to calculate midpoints with both positive and negative coordinates.
• 😀 Midpoints can be represented in decimals or fractions depending on preference.
• 😀 Practical exercises include finding midpoints for scenarios like drones, hikers, and ships.
• 😀 Life application questions connect the midpoint concept to friendship and teamwork, emphasizing meeting halfway and sharing responsibilities.
• 😀 Visualizing midpoints on a Cartesian plane helps in understanding their location relative to points.
• 😀 The video encourages students to practice independently and provides resources like PowerPoint presentations for further learning.

Q & A

What is the main topic of the lesson in the video?

The main topic of the lesson is the midpoint of a line segment on the Cartesian coordinate plane.

What is the formula for finding the midpoint of a line segment?

The midpoint formula is M = ((x1 + x2)/2, (y1 + y2)/2), where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.

How can you find the midpoint between two horizontally aligned points?

For horizontally aligned points, add the x-coordinates of the two points, divide by 2 to get the x-coordinate of the midpoint, and use the common y-coordinate as the midpoint's y-coordinate.

How is the midpoint calculated for two vertically aligned points?

For vertically aligned points, add the y-coordinates of the two points, divide by 2 to get the y-coordinate of the midpoint, and use the common x-coordinate as the midpoint's x-coordinate.

How do you determine the midpoint if the points are diagonally aligned?

Use the midpoint formula by adding the x-coordinates and dividing by 2 for the x-coordinate, and adding the y-coordinates and dividing by 2 for the y-coordinate, regardless of diagonal alignment.

Why did the video use a scenario of friends meeting halfway between their houses?

The scenario was used to illustrate the practical application of finding a midpoint, showing how it represents a fair meeting point equidistant from two locations.

What are the midpoint coordinates for Anna and Carlos in the example?

The midpoint coordinates for Anna and Carlos are (-2, 1).

What are the answers to the practice exercises involving the drone, hikers, and ship?

The midpoint coordinates are: Drone path: (1, 1), Hikers: (3.5, -6.5), Ship journey: (-30, -25).

How can understanding midpoints be applied to teamwork and relationships?

Meeting halfway in friendship or sharing responsibilities in teamwork reflects the concept of a midpoint, promoting fairness, balance, and stronger relationships.

What advice does the video give for students to further practice and understand midpoints?

Students are encouraged to try the exercises on their own, plot points on the Cartesian plane, and comment their insights or answers for feedback.

What previous lesson is reviewed to help understand midpoints?

The video reviews the lesson on calculating the distance between two points on the Cartesian plane, which helps in understanding spatial relationships needed to find midpoints.

Can midpoint coordinates be expressed as fractions or decimals?

Yes, midpoint coordinates can be expressed either as fractions or decimals depending on preference or the context of the problem.