Volume de pirâmide - Brasil Escola
Summary
TLDRIn this math lesson, the teacher explains how to calculate the volume of a pyramid. By comparing a pyramid with a rectangular base to a rectangular prism, the teacher demonstrates that the volume of the pyramid is one-third of the volume of the prism. Using a clear example with a regular square-based pyramid, the teacher walks through the steps: calculating the area of the base, multiplying by the height, and dividing by three to get the volume. The video also suggests reviewing previous lessons on pyramid areas for a better understanding.
Takeaways
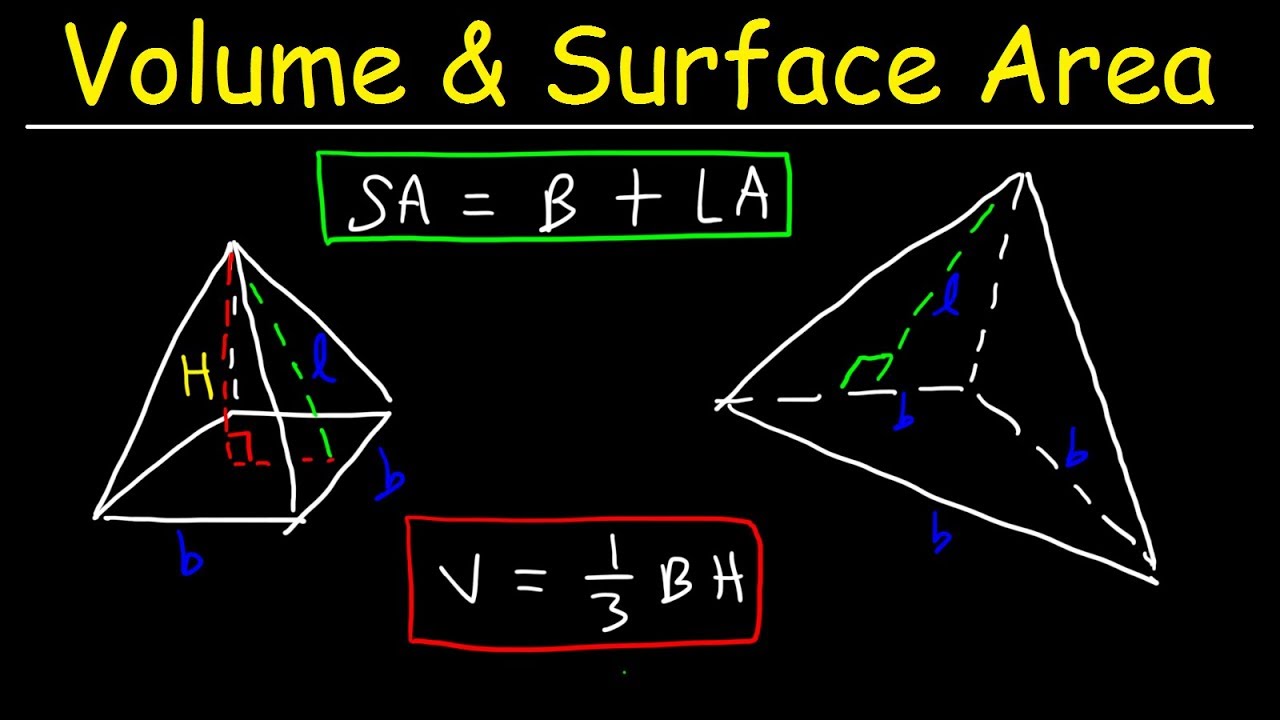
- 😀 The volume of a pyramid is calculated using the formula: Volume = (Area of base * Height) / 3.
- 😀 To understand the volume relationship between a pyramid and a prism, the volume of a prism is three times that of a pyramid with the same base area and height.
- 😀 The formula for the volume of a pyramid is derived from the fact that three pyramids with the same base area and height can fit into a prism.
- 😀 The volume of a pyramid is always one-third of the volume of a corresponding prism, where the prism has the same base and height as the pyramid.
- 😀 The area of the base of a pyramid can be calculated first, then multiplied by the pyramid's height to find the volume before dividing by 3.
- 😀 The script uses a practical example of a pyramid with a square base to explain the volume calculation.
- 😀 In the example, the diagonal of the square base is given as 24√2 cm, and from this, the side of the square can be determined.
- 😀 To calculate the area of the base for a square pyramid, the side length is squared, and then the result is used in the volume formula.
- 😀 In the example, after calculating the area of the square base and multiplying it by the height of the pyramid, the final volume is obtained by dividing by 3.
- 😀 The final volume of the pyramid in the example is found to be 3,072 cubic centimeters, demonstrating the application of the formula.
Q & A
What is the main topic of this lesson?
-The main topic of the lesson is how to calculate the volume of a pyramid.
How do we calculate the volume of a pyramid in this video?
-The volume of a pyramid is calculated as one-third of the base area times the height, which is expressed as: Volume = (Base Area * Height) / 3.
What visual aid does the teacher use to explain the concept?
-The teacher uses a visual comparison between a rectangular prism and a pyramid, showing how three pyramids can fit inside the prism, illustrating the relationship between their volumes.
What formula is derived to calculate the volume of a pyramid?
-The formula derived for the volume of a pyramid is: Volume = (Base Area * Height) / 3.
What is the significance of the number three in the volume calculation?
-The number three signifies that the volume of the pyramid is one-third of the volume of a prism with the same base area and height. This is why the pyramid's volume is calculated by dividing the prism's volume by three.
How does the teacher suggest remembering the formula for the volume of a pyramid?
-The teacher suggests remembering that the volume of a pyramid is one-third of the volume of a prism, and that the formula is: Volume = (Base Area * Height) / 3.
What exercise does the teacher work through in the video?
-The teacher works through an exercise where the base of a pyramid is a square, and the diagonals of the base are 24√2 cm. The height of the pyramid is 16 cm, and the goal is to calculate the volume of the pyramid.
How does the teacher calculate the side length of the square base?
-The teacher uses the fact that the diagonal of a square is equal to the side length times the square root of 2. Given the diagonal is 24√2 cm, the teacher simplifies it to find that the side length of the square is 24 cm.
What steps are involved in calculating the volume of the pyramid in the exercise?
-First, the side length of the square base is found (24 cm). Then, the area of the base is calculated by squaring the side length (24 * 24). Finally, the area is multiplied by the height of the pyramid (16 cm) and divided by three to find the volume.
What is the final volume of the pyramid in the exercise?
-The final volume of the pyramid is 3,072 cubic centimeters.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)