Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
Summary
TLDREn este video, Salvatore presenta un análisis detallado de las medidas de posición en estadística, incluyendo cuartiles, deciles y percentiles, aplicados tanto a datos agrupados como no agrupados. Comienza explicando cómo calcular los cuartiles sin fórmulas, usando la mediana de los datos ordenados. Luego, aborda el cálculo de deciles y percentiles mediante fórmulas específicas para cada caso. A lo largo de la explicación, Salvatore usa ejemplos prácticos para ilustrar cómo determinar posiciones y valores de estos indicadores, brindando una comprensión clara y accesible de estos conceptos clave en estadística.
Takeaways
- 😀 Las medidas de posición dividen un conjunto de datos en partes iguales, y las más importantes son los cuartiles, deciles y percentiles.
- 😀 Los cuartiles dividen los datos en cuatro partes iguales, los deciles en diez partes y los percentiles en cien partes.
- 😀 Para calcular los cuartiles en datos no agrupados, primero se ordenan los datos y se encuentran las medianas para cada cuartil.
- 😀 Los cuartiles 1 y 3 se encuentran como medianas de las mitades inferior y superior de los datos, respectivamente.
- 😀 En el caso de tener un número par de datos, se calcula la media de los dos valores centrales para encontrar la mediana.
- 😀 Para los deciles y percentiles en datos no agrupados, se utiliza una fórmula para calcular la posición, la cual depende del total de datos y el índice de decil o percentil que se desea calcular.
- 😀 El cálculo de la posición de un decil o percentil implica multiplicar el índice por el total de datos y dividirlo entre el número de partes (10 para deciles y 100 para percentiles).
- 😀 Al calcular un decil o percentil, si la posición calculada no es un número entero, se debe interpolar entre los dos valores cercanos.
- 😀 Para datos agrupados, se utilizan fórmulas similares, pero se deben considerar los límites de clase, la frecuencia acumulada y la amplitud de la clase para encontrar el cuartil, decil o percentil.
- 😀 En los datos agrupados, se calcula la frecuencia acumulada y la amplitud de cada clase antes de aplicar la fórmula para encontrar el valor deseado de cuartil, decil o percentil.
Q & A
¿Qué son las medidas de posición?
-Las medidas de posición son aquellas que dividen un conjunto de datos en partes iguales. Las más importantes son los cuartiles, deciles y percentiles.
¿Cuáles son los tres tipos principales de medidas de posición mencionados en el video?
-Los tres tipos principales de medidas de posición son los cuartiles, deciles y percentiles.
¿Cuál es la diferencia entre datos agrupados y no agrupados?
-Los datos no agrupados son aquellos que están listados de manera individual, mientras que los datos agrupados están organizados en intervalos, como se muestra en una tabla.
¿Cómo se calculan los cuartiles para datos no agrupados?
-Para calcular los cuartiles en datos no agrupados, primero se ordenan los datos de menor a mayor, luego se divide el conjunto en cuatro partes iguales, y las medianas de cada sección corresponden a los cuartiles.
¿Qué fórmula se utiliza para calcular la posición de un decil?
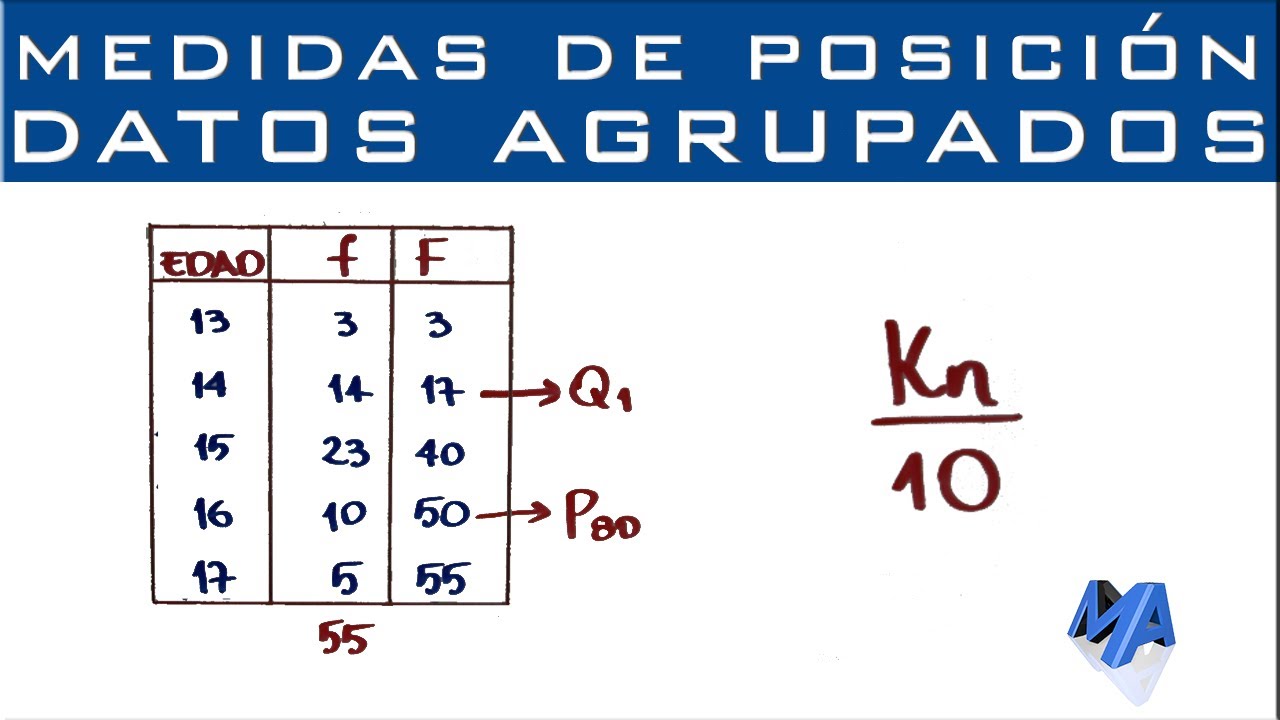
-Para calcular la posición de un decil, se utiliza la fórmula: (k * n) / 10, donde k es el número del decil que se desea calcular y n es el total de datos.
En el cálculo de deciles, ¿por qué se divide por 10?
-Se divide por 10 porque los deciles dividen el conjunto de datos en 10 partes iguales, lo que significa que se hacen 9 cortes.
¿Cómo se calcula la posición de un percentil?
-La fórmula para calcular la posición de un percentil es similar a la de los deciles, pero se utiliza 100 en lugar de 10, ya que los percentiles dividen el conjunto de datos en 100 partes iguales.
¿Qué se debe hacer antes de aplicar cualquier fórmula para calcular las medidas de posición?
-Antes de aplicar las fórmulas para calcular las medidas de posición, es necesario ordenar los datos de menor a mayor.
¿Cuál es la diferencia entre cuartil 1, cuartil 2 y cuartil 3?
-El cuartil 1 (Q1) es la mediana de la primera mitad de los datos, el cuartil 2 (Q2) es la mediana de todo el conjunto de datos (también conocida como la mediana general), y el cuartil 3 (Q3) es la mediana de la segunda mitad de los datos.
¿Cómo se calculan los cuartiles para datos agrupados?
-Para datos agrupados, se utilizan fórmulas que consideran el límite inferior de la clase, la frecuencia acumulada, la frecuencia absoluta y la amplitud de la clase. Se calcula la posición usando estas variables y luego se obtiene el valor del cuartil a partir de la clase correspondiente.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS

CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente

Conceptos estadísticos básicos

Cuartiles, deciles y percentiles Definición e interpretaciones
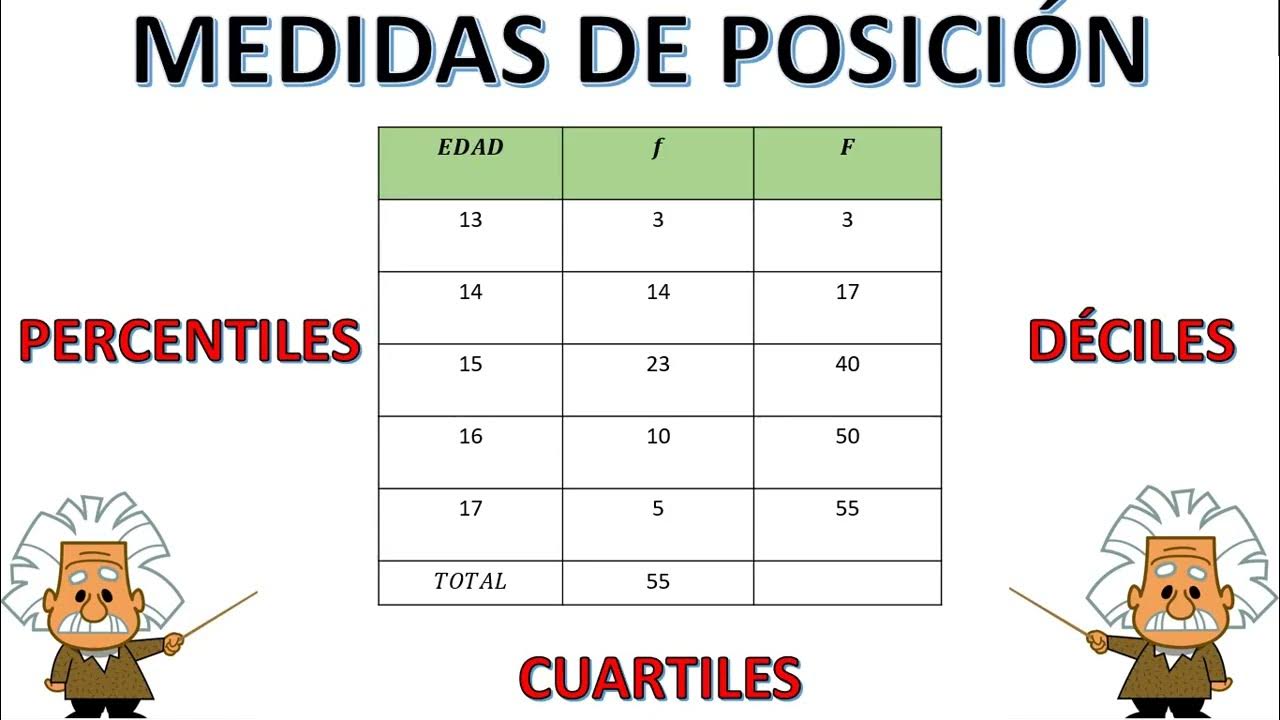
MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles
5.0 / 5 (0 votes)
