El gradiente de una función - concepto e interpretación
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
Was ist der Gradient einer Funktion und was stellt er dar?
-Der Gradient einer Funktion ist ein Vektor, der die Richtung und die Größe der größten Änderung einer Skalarfeldfunktion beschreibt. Er zeigt an, wie schnell sich die Funktion an einem bestimmten Punkt in Bezug auf ihre Variablen verändert.
Welche Bedeutung hat die Differenzierbarkeit einer Funktion für den Gradienten?
-Eine Funktion muss differenzierbar sein, um einen Gradienten zu besitzen. Dies bedeutet, dass die Funktion an diesem Punkt stetig und ableitbar ist, was notwendig ist, um die partiellen Ableitungen, die den Gradient bilden, zu berechnen.
Wie berechnet man den Gradienten einer Funktion von zwei Variablen?
-Der Gradient einer Funktion f(x, y) von zwei Variablen wird durch die partiellen Ableitungen von f bezüglich x und y berechnet: ∇f = (∂f/∂x, ∂f/∂y).
Was beschreibt der Gradient physikalisch?
-Physikalisch beschreibt der Gradient die Richtung der größten Zunahme einer Funktion. Er gibt an, in welche Richtung die Funktion am schnellsten ansteigt, und die Größe des Gradienten gibt die Steigung in dieser Richtung an.
Was sind Kurven und Flächen des gleichen Wertes einer Funktion und wie hängen sie mit dem Gradienten zusammen?
-Kurven oder Flächen des gleichen Wertes einer Funktion werden als Niveaukurven oder -flächen bezeichnet. Der Gradient einer Funktion ist immer senkrecht zu diesen Niveaukurven oder -flächen, was bedeutet, dass der Gradient die Richtung des größten Anstiegs der Funktion anzeigt, während die Niveaukurven Orte konstanten Funktionswertes sind.
Warum ist der Gradient senkrecht zur Tangente der Niveaukurve?
-Der Gradient ist senkrecht zur Tangente der Niveaukurve, weil der Gradient die Richtung maximaler Veränderung der Funktion beschreibt, während die Tangente eine Richtung mit null Veränderung der Funktion darstellt. Dies wird durch das Skalarprodukt der beiden Vektoren gezeigt, das null ist.
Wie wird der Gradient einer Funktion in drei Dimensionen dargestellt?
-Der Gradient einer Funktion in drei Dimensionen, f(x, y, z), wird durch die partiellen Ableitungen von f bezüglich x, y und z berechnet: ∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z). Dieser Vektor zeigt die Richtung der größten Veränderung der Funktion im 3D-Raum an.
Was passiert mit dem Gradient einer Funktion, wenn die Funktion in drei Dimensionen eine Oberfläche definiert?
-Wenn eine Funktion in drei Dimensionen eine Oberfläche definiert, ist der Gradient der Funktion an jedem Punkt der Vektor, der senkrecht zum Tangentialebene der Oberfläche im betrachteten Punkt steht. Dies bedeutet, dass der Gradient als Normalenvektor zur Oberfläche fungiert.
Wie wird der Gradient der Funktion f(x, y, z) = x² + y² - z = 0 berechnet und was zeigt seine Darstellung in 3D?
-Der Gradient der Funktion f(x, y, z) = x² + y² - z = 0 wird als Vektor ∇f = (2x, 2y, -1) berechnet. In 3D zeigt die Darstellung des Gradienten, dass der Vektor in jedem Punkt der Oberfläche senkrecht zur Ebene ist, die die Tangente darstellt.
Welche Bedeutung hat der Gradient bei der Analyse von Funktionen, die in zwei oder drei Dimensionen definiert sind?
-Der Gradient ist ein fundamentales Werkzeug zur Analyse von Funktionen in mehreren Dimensionen. Er hilft, die Richtungen zu bestimmen, in denen die Funktion am schnellsten wächst, und wird verwendet, um Eigenschaften wie Steigungen, max. Wachstumsrichtungen und das Verhalten der Funktion im Raum zu untersuchen.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Osmotic pressure, definition and control

INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA, CÁLCULO DIFERENCIAL
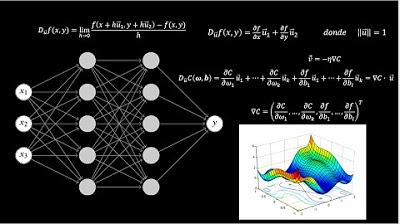
Las Matemáticas detrás de la IA

Ejemplo de cálculo del laplaciano | Cálculo multivariable | Khan Academy en Español

Del perceptrón a la red neuronal

Derivadas direccionales de un campo escalar | 26/41 | UPV

Pensamiento matemático 3. Progresión 1b. Variación promedio
5.0 / 5 (0 votes)