Las Matemáticas detrás de la IA
Summary
TLDREste video explica de manera sencilla el concepto de redes neuronales artificiales, comenzando con las primeras ideas en los años 50, como el perceptrón de Rosenblatt. Utiliza ejemplos para ilustrar cómo estas redes funcionan con entradas, salidas y pesos, y cómo pueden aprender ajustando estos pesos. Además, describe cómo evolucionaron los modelos multicapa, incorporando la función sigmoide para suavizar las salidas. También se aborda el proceso de minimización de errores utilizando el gradiente descendente. Finalmente, se ejemplifica cómo una red neuronal aprende a representar una función matemática compleja.
Takeaways
- 🤖 Las primeras ideas sobre redes neuronales surgieron en los años 50, con Frank Rose y los trabajos previos de Warren McCulloch y Walter Pitts.
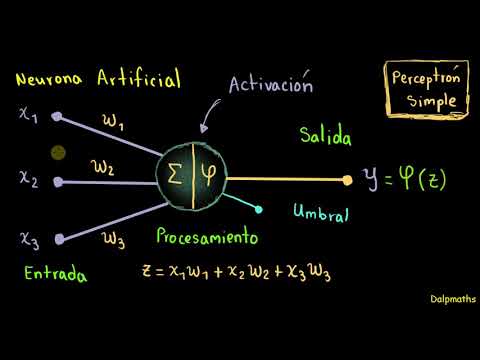
- 🔧 Un perceptrón es un modelo simple basado en neuronas biológicas, con entradas y una única salida.
- ⚙️ El perceptrón utiliza pesos para determinar la importancia de cada entrada en la salida, y estos pueden ajustarse según los resultados esperados.
- 🧠 Las redes neuronales aprenden ajustando los pesos a través de algoritmos para reducir los errores en las salidas.
- 🎛️ El modelo de perceptrón multicapa introduce varias capas de neuronas, conectadas entre sí, con funciones de activación como la sigmoide.
- 📊 La función de coste mide qué tan cerca está la salida obtenida de la salida esperada, y se minimiza para mejorar el aprendizaje.
- ⚡ La derivada direccional y el gradiente son herramientas clave para ajustar los pesos y minimizar la función de coste.
- 📉 Al desplazarse en la dirección inversa del gradiente, el sistema puede reducir el error y optimizar la red neuronal.
- 🧩 Las redes neuronales modernas utilizan la función sigmoide para suavizar las transiciones en los valores de salida, mejorando la precisión.
- 🔍 Aunque las redes neuronales pueden aprender patrones complejos, calcular el gradiente de la función de coste puede ser complicado y requiere más análisis.
Q & A
¿Qué significó la tecnología de las redes neuronales en los últimos tiempos?
-La tecnología de las redes neuronales ha representado un avance significativo en el ámbito de la inteligencia artificial, permitiendo a las máquinas aprender y realizar tareas de manera autónoma.
¿Quién fue Frank Rosen y qué aportó a la creación de las redes neuronales?
-Frank Rosen fue un investigador que, inspirado por trabajos anteriores de Warren Sturgis McCulloch y Walter Pitts, creó las primeras ideas de las redes neuronales basadas en un modelo llamado perceptrón.
¿Qué es un perceptrón y cómo funciona?
-Un perceptrón es un modelo de red neurál artificial que se basa en neuronas biológicas. Funciona como una caja con entradas y salidas, donde se pueden modificar los controles centrales para alterar la salida según los valores de entrada.
¿Cuál es la diferencia entre una red neuronal simple y una multicapa?
-Una red neuronal simple es un perceptrón que procesa la información de entrada directamente a una salida. Una red multicapa, por otro lado, es un conjunto de percepciones donde cada capa está conectada a la siguiente y cada neurona comparte su salida con todas las neuronas de la capa siguiente.
¿Qué son los pesos en el contexto de las redes neuronales y para qué sirven?
-Los pesos son valores reales que representan la importancia de cada entrada en la producción de la salida esperada. Sirven para ajustar la salida de la red neuronal de acuerdo con la configuración de los controles.
¿Cómo se determina si un perceptrón debe activarse o no?
-Un perceptrón se activa si la suma del producto de los pesos y las entradas supera un umbral determinado. De lo contrario, no se activa.
¿Qué es la función sigmoide y cómo se utiliza en las redes neuronales?
-La función sigmoide es una función matemática que transforma la salida de un perceptrón simple en un número real entre 0 y 1. Se utiliza para suavizar la salida y proporcionar una salida continua en lugar de un cambio brusco de 0 a 1.
¿Cómo se aprende una red neuronal a minimizar los errores?
-Las redes neuronales aprenden minimizando la función de coste, que es una medida de la diferencia entre la salida obtenida y la esperada. Se hace ajustando los pesos de la red neuronal en la dirección inversa al gradiente de la función de coste.
¿Qué es el gradiente descendente y cómo ayuda en el aprendizaje de las redes neuronales?
-El gradiente descendente es un método para encontrar el mínimo de una función, en este caso, la función de coste de la red neuronal. Consiste en desplazarse en la dirección opuesta al gradiente, lo que lleva a una disminución de la función de coste y, por tanto, a un aprendizaje más eficiente.
¿Por qué es importante minimizar los errores en el aprendizaje de las redes neuronales?
-Minimizar los errores es fundamental para que las redes neuronales aprendan patrones y realicen predicciones con alta precisión. Menos errores significan que la salida de la red neuronal se acerca más a la salida esperada.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)