The Mathematical Code Hidden In Nature
Summary
TLDRThis script explores the mathematical underpinnings of nature's patterns, focusing on Alan Turing's 'reaction-diffusion' theory. It reveals how simple equations can explain complex biological phenomena like zebra stripes and leopard spots. Despite initial skepticism, Turing's work has been validated by recent biological discoveries of actual 'morphogens'. The narrative also poignantly touches on Turing's tragic life and his profound contributions to both computing and biology, emphasizing the beauty and power of mathematics in understanding our world.
Takeaways
- 🧬 The diversity of life's patterns can be explained by simple mathematical equations, challenging the notion that biology is too complex and unpredictable for such simplicity.
- 🦓 The mystery of zebra stripes is not just about camouflage but also serves to confuse biting flies, highlighting the multifaceted purposes of biological patterns.
- 🔢 Alan Turing's mathematical model, known as 'Turing patterns', provides a framework for understanding how complex biological patterns emerge from simple chemical interactions.
- 🌐 Turing's work in mathematical biology was initially overlooked, possibly due to the overshadowing of DNA's discovery and the skepticism towards a mathematician's contribution to the field.
- 🧪 The concept of 'morphogens', as introduced by Turing, refers to chemicals that spread and react differently to create various biological patterns, a key to understanding morphogenesis.
- 🔄 The reaction-diffusion equations describe how two chemicals interact and spread, leading to the formation of patterns like those seen on animals' skins.
- 🐆 By adjusting variables in Turing's equations, such as the rate of chemical production and diffusion, different patterns like spots or stripes can be generated.
- 🌱 The rediscovery of Turing patterns in the 1970s by Gierer and Meinhardt spurred further interest in applying mathematics to understand biological development.
- 🔬 Recent biological findings have identified actual morphogens, supporting Turing's theories and demonstrating the practical application of his mathematical models in nature.
- 💡 Turing's legacy extends beyond his mathematical and computational contributions, as his work in biology has inspired new avenues of research and deepened our understanding of life's complexity.
Q & A
What is the mystery underlying the variety of patterns in the living world?
-The mystery is how such a variety of patterns, like spots and stripes, can arise from the same simple biological building blocks: cells and their chemical instructions.
What is a Turing pattern and who discovered it?
-A Turing pattern is a set of patterns in nature, such as spots, stripes, and waves, that can be explained by a set of mathematical equations. They were discovered by mathematician Alan Turing in 1952.
Why were Turing's ideas initially ignored when he published his work on biological patterns?
-Turing's ideas were largely ignored at the time of publication possibly because they were overshadowed by other significant discoveries in biology, such as the double helix structure of DNA, or because the scientific community was not yet ready to accept mathematical explanations for biological phenomena.
What is 'morphogenesis' and how does it relate to Turing's work?
-Morphogenesis is the biological process that causes an organism to develop its shape. Turing's work is related to this process as he published a paper called 'The Chemical Basis of Morphogenesis' which included equations describing how complex shapes can arise spontaneously from simple initial conditions.
What is a reaction-diffusion system and how does it create patterns?
-A reaction-diffusion system is a model that involves two or more chemicals moving around and reacting with each other. It creates patterns by having one chemical (the activator) that promotes its own production and the production of an inhibitor, while the second chemical (the inhibitor) suppresses the activator. The interaction and diffusion of these chemicals can lead to the formation of various patterns.
How do the concepts of activator and inhibitor chemicals relate to the formation of biological patterns?
-In the context of biological pattern formation, the activator chemical promotes its own production and that of an inhibitor, while the inhibitor chemical suppresses the activator. This interplay, along with the differential rates of diffusion of these chemicals, can lead to the formation of various patterns such as spots or stripes.
How did Turing's mathematical models predict the patterns on a cheetah's fur?
-Turing's models predicted patterns by simulating a reaction-diffusion system where an activator (like a fire) and an inhibitor (like firefighters) interact. The activator promotes its own production, while the inhibitor suppresses it. The key to getting spots, as opposed to a uniform color, is that the inhibitor diffuses faster than the activator.
What role did Alan Turing play in World War II and the development of computer science?
-Alan Turing was a famous wartime codebreaker who played a significant role in decoding the Enigma machine, which is estimated to have shortened World War II in Europe by more than two years. After the war, he was instrumental in developing the core logical programming that forms the basis of modern computers.
What challenges did Turing face in his lifetime, and how were they related to his work?
-Alan Turing faced significant personal challenges, including criminal charges for being in a homosexual relationship at a time when it was illegal in the UK. He chose chemical castration treatment over prison, but tragically died from cyanide poisoning two years after his treatment began, likely a suicide. These challenges were unrelated to his scientific work but tragically cut short a brilliant career.
How have biologists verified Turing's mathematical models in the context of actual biological systems?
-Biologists have verified Turing's models by finding actual morphogens—chemicals or proteins inside cells—that behave as his model predicts. Examples include patterns on a mouse's mouth, bird feathers, human arm hair, and shark denticle scales, all of which are sculpted by the diffusion and reaction of molecular morphogens.
What is the significance of Turing's work in the field of biology and mathematics?
-Turing's work is significant because it demonstrated that mathematics could be used to explain complex biological patterns, leading to a new field of study called mathematical biology. His work has inspired new questions and approaches in understanding the underlying processes of biological development and pattern formation.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
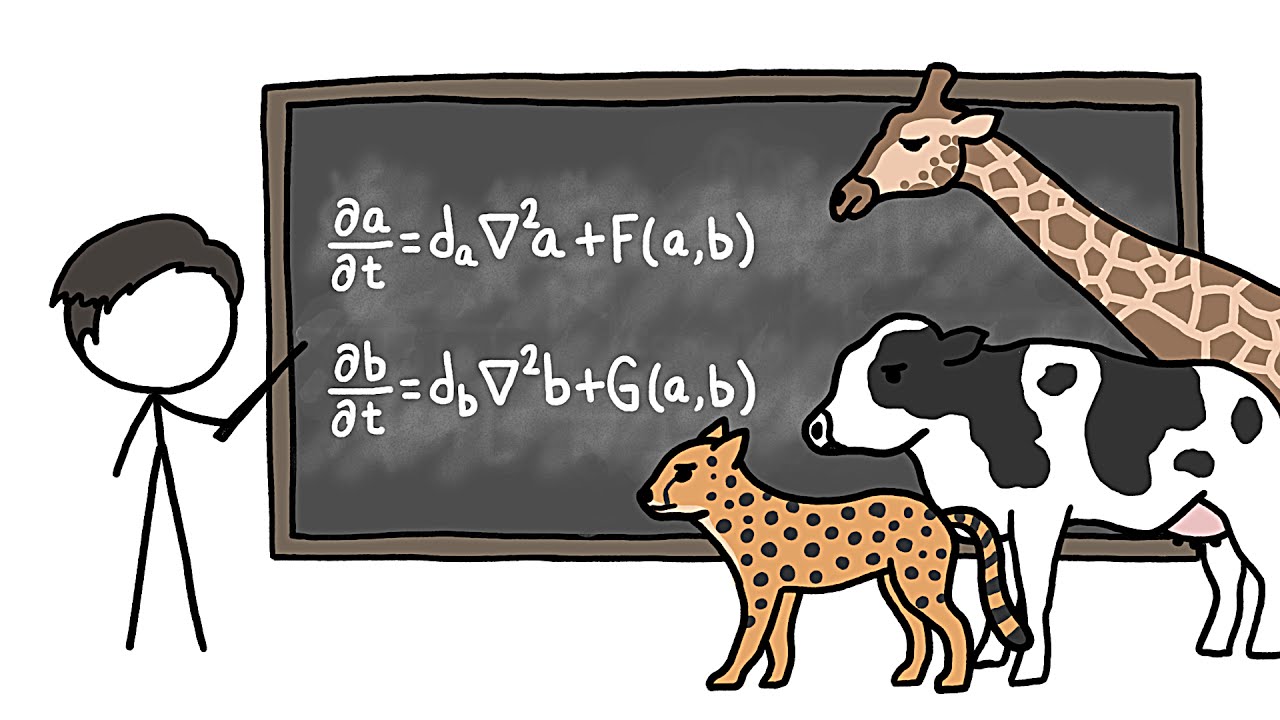
Can Math Explain How Animals Get Their Patterns?

PART 3: PATTERNS AND NUMBERS IN NATURE AND THE WORLD || MATHEMATICS IN THE MODERN WORLD

APAKAH TUHAN AHLI MATEMATIKA??

Laju Reaksi (3) | Faktor Yang mempengaruhi Laju Reaksi | Teori Laju Reaksi

OS COMPUTADORES HERÓIS da Segunda Guerra Mundial #SagaDosComputadores Ep. 3

NATURES MATHEMATICS PART-1 1080p HD DOCUMENTARY
5.0 / 5 (0 votes)
